On this page we'll cover both planes tangent to three-dimensional functions defined as $z = f(x,y)$ (main body of this page) and surfaces defined parametrically, such as the vector function $\vec r(u,v)=x(u,v)\, \hat i+ y(u,v) \, \hat j + z(u,v)\,\hat k$ below.
Linear approximation in single-variable calculus
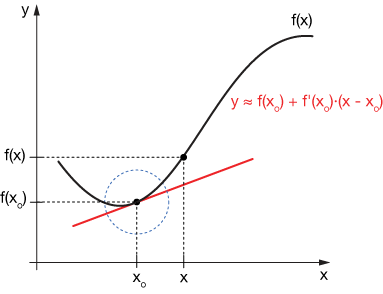
We've already learned how single-variable calculus — specifically, calculating the slope of a curve at a point, $x_o$ in its domain — can help us to quickly approximate the value of the function in the neighborhood of $x_o$. The graph shows such a scenario.
The key is to calculate the slope of the function at a point $x_o$. Then in the neighborhood (like inside of the blue-dashed circle) of that point, our linear approximation of the value of our function at some new point, $x$, is $f(x_o)$ plus that slope multiplied by the distance from $x$ to $x_o$.
$$f(x) \approx f(x_o) + f'(x_o)(x - x_o)$$
Any curved function $f(x)$, when viewed closely enough, is approximately linear, so this approximation works better the closer $x$ is to $x_o$.
In this section we'll generalize this concept to finding the equation of a plane tangent to 3D function $f(x,y)$. The ideas are similar, and they involve partial derivatives — rates of change of 3D functions in the $x$- and $y$-dimensions.
Simple example — tangent to a sphere
As a first example, let's look at the equation of a plane tangent to a sphere. Let's take an easy sphere, the sphere of radius 3 centered at the origin:
$$x^2 + y^2 + z^2 = 9$$
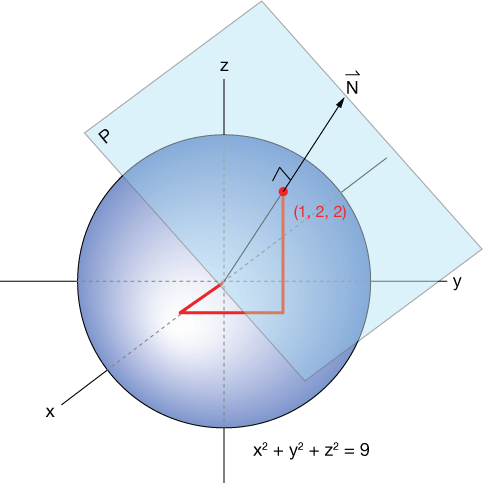
and find an equation of the plane tangent to it at $(1, 2, 2)$. You can confirm for yourself that $(1, 2, 2)$ is on the sphere.
Now the radius vector of any sphere is normal to the sphere where it intersects it*, so our vector $\vec N = (1, 2, 2)$ is a normal vector at point $(1, 2, 2)$ on the surface of the sphere. In the diagram, we've drawn that vector twice, once inside the sphere and once outside of it, just to provide some perspective.
Now the equation of a plane is
$$a(x - x_o) + b(y - y_o) + c(z - z_o) = 0,$$
where $(a, b, c)$ is the normal vector, and in this case, $(x_o, y_o, z_o) = (1, 2, 2)$. So our plane equation is
$$ \begin{align} 1(x - 1) + 2(y - 2) + 2(z - 2) &= 0 \\[5pt] x - 1 + 2y - 4 + 2z -4 &= 0 \\[5pt] x + 2y + 2z &= 9 \end{align}$$
Now we won't always have such a neat situation — where we know the normal vector going in — so we'll develop a more generally useful method next.
* This is the analog from that rule you learned in plane geometry: The tangent to a circle is perpendicular to the radius that meets the point of tangency.
Tangent planes
In order to find an equation of a plane tangent to a function $f(x,y)$, we need
- A point on the surface of $f(x,y)$ which will also be on our plane
- A normal vector $\vec n$
The equation of our plane must obey the dot product $\vec n \cdot \vec{P_o P} = 0$, where $\vec{P_oP}$ is a vector in the plane. The coordinates of $P_o$ and $P$, respectively, are $(x_o, y_o, z_o)$ and $(x,y,z)$. The equation of our plane has the form
$$a(x - x_o) + b(y - y_o) + c(z - z_o) = 0,$$
where $\vec n = (a, b, c)$. Because there are an infinite number of equations for a plane, we can let $c$ be any nonzero number. Let's use $c = -1$, which will turn out to be a convenient choice. Then our equation changes to
$$a(x - x_o) + b(y - y_o) + z_o = z$$
Notice that this is a linear function for $L(x,y)$ — linear in variables $x$ and $y$. Then if we let $y = y_o$, we have
$$a(x - x_o) + z_o = z,$$
which is the equation of a parallel to the $xz$ plane with slope $a$. Its linear approximation requires the derivative of the function in that plane ($y$ constant): $a = \frac{\partial f}{\partial x}(x_o, y_o)$. Likewise, if we let $x = x_o$, then we have
$$b(y - y_o) + z_o = z,$$
an equation of a line in the $yz$ plane for which $b = \frac{\partial f}{\partial y}(x_o,y_o)$. Substituting these expressions for $a$ and $b$, we get
$$f_x (x_o,y_o) (x - x_o) + f_y (x_o,y_o)(y - y_o) + z_o = z,$$
an easy way to find a plane tangent to $f(x,y)$ at $(x_o, y_o, z_o)$.
Tangent plane in $\mathbb{R}^3$
The equation of a plane tangent to $f(x,y)$ at $(x_o, y_o)$ is
$$z = \frac{\partial f}{\partial x} (x - x_o) + \frac{\partial f}{\partial y} (y - y_o) + z_o$$
or
$$z = f_x (x - x_o) + f_y (y - y_o) + z_o$$
Another path to tangent planes
Here's another path to the tangent plane equation. You might find this one more palatable — up to you. Consider the surface and plane below:
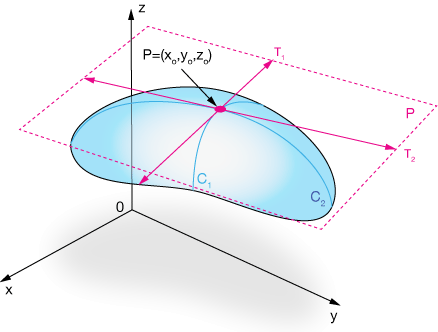
The surface is given by $z = f(x, y)$ and the point of tangency of our plane is $P = (x_o, y_o, z_o)$. That means that our plane will have the equation
$$A(x-x_o) + B(y-y_o) + C(z-z_o) = 0$$
Now we can employ a trick: Divide through by $C$ and isolate $z-z_o$:
$$z-z_o = -\frac{A}{C} (x-x_o) - \frac{B}{C}(y-y_o)$$
Now $A, \; B$ and $C$ are unspecified right now, so we can make the replacement,
$$a = -\frac{A}{C} \phantom{0000} -\frac{B}{C} = b$$
So the equation of our tangent plane is
$$z-z_o = a(x-x_o) + b(y-y_o)$$
Now let's let $y = y_o$, which will convert our equation to
$$z-z_o = a(x-x_o)$$
This is the point-slope formula for the tangent $T_1$ in the $y$-$z$ plane, which means that $a$ is the slope in that direction, or $a = \frac{\partial f}{\partial x}$. We can make the same argument for the constant $b$ by setting $x=x_o$: $b = \frac{\partial f}{\partial y}$. If we call these partial derivatives $f_x$ and $f_y$ for short, our final tangent plane equation is
$$z-z_o = f_x(x_o, y_o)(x - x_o) + f_y(x_o, y_o)(y - y_o)$$
Example 1
Find the equation of the plane tangent to the function $f(x,y) = -x^2 - y^2$ at the point $(x,y) = (1, 1)$. Use the resulting plane to approximate the value of $f(0.95, 1.05)$ and compare it to the exact result.
The partial derivatives are
$$ \begin{align} f_x = -2x \; \rightarrow \; f_x(1,1) &= -2 \\[5pt] f_y = -2y \; \rightarrow \; f_y(1,1) &= -2 \end{align}$$
So our plane equation is
$$ \begin{align} z &= -2(x-1) - 2(y-1) -2 \\[5pt] &= -2x + 2 -2y + 2 -2 \\[5pt] &= -2x - 2y - 2 \end{align}$$
or $ \phantom{000}2x + 2y + z = 2$.
We can read the normal vector straight from this equation, $\vec n = (2, 2, 1)$. Here are 3D plots of our function and its tangent plane, one from the side so you can see the point of tangency (
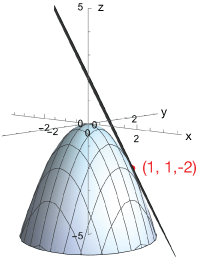
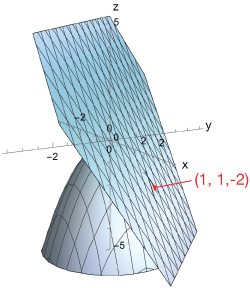
Approximation
The tangent plane is a good approximation in the region around $(x, \; y) = (1, \; 1)$ Using the equation of the plane, $z(0.95, 1.05) is
$$ \begin{align} z(0.95, 1.05) &= -2(0.95) - 2(1.05) + 2 \\[5pt] &= -1.90 - 2.10 + 2 \\[5pt] &= -2.0 \end{align}$$
The more exact value is
$$ \begin{align} z(0.95, 1.05) &= -(0.95)^2 - (1.05)^2 \\[5pt] &= -0.9025 - 1.1025 \\[5pt] &= -2.005 \end{align}$$
So the approximation at this point is pretty good — to about ½ percent.
Example 2
Find the equation of the plane tangent to $f(x,y) = x^3 + xy^2 - y + 4$ at $(x,y) = (1,2)$.
The partial derivatives are
$$ \begin{align} f_x = 3x^2 + y^2 \; \rightarrow \; f_x(1,2) &= 3+4=7 \\[5pt] f_y = 2xy - 1 \; \rightarrow \; f_y(1,2) &= 4-1 = 3 \end{align}$$
So our plane equation is
$$ \begin{align} z &= 7(x-1) + 3(y-2) + 7 \\[5pt] &= 7x - 7 + 3y - 6 + 7 \\[5pt] &= 7x + 3y - 6 \end{align}$$
or $ \phantom{000}7x + 3y - z = -6$.
We can read the normal vector straight from this equation, $\vec n = (7,3,-1)$. Here is a 3D plot of our function and its tangent plane. This is a trick graph because the tangent plane intersects with the curved surface near our chosen point of tangency.
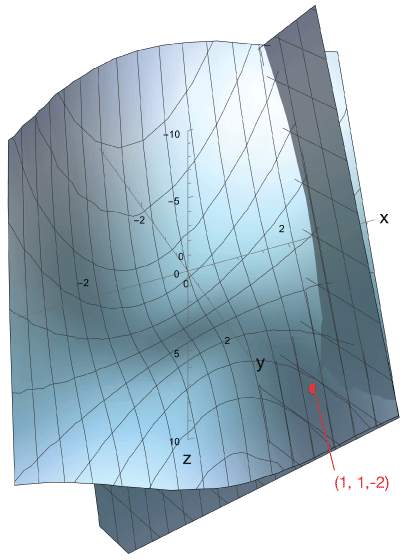
Another way to think about it: The gradient
Here's a schematic of a made-up function in $\mathbb{R}^3$. The function might be written as $z = f(x,y)$, but we could also write it as $F(x,y,z) = 0$. Just as a quick example, consider the function $f(x) = x^2 - y^2 + 3$. That's really $z = x^2 - y^2 + 3$, which we could also write as $z - x^2 + y^2 - 3 = 0$.
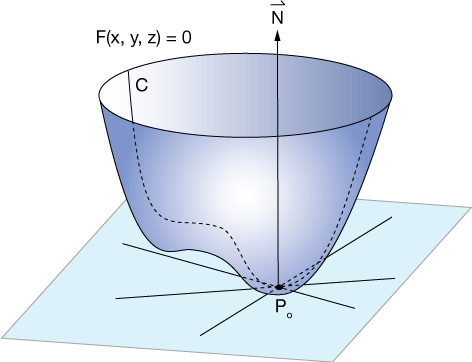
Now consider the point $P_o$ on the plane that's meant to be tangent to $f(x,y)$ at that point. If that plane is really tangent to the 3D curve, then it consists of all possible tangents to the curve at that point. Let's focus on one of those, the tangent to the curve $C$, one of many that traces the 3D graph and passes through $P_o$. We're going to claim that
$$\vec N = \nabla \vec F = (F_x, F_y, F_z),$$
where $\vec N$ is normal to the plane and any line in it, and $\nabla$ is the gradient "operator". Is our claim true?
We can define the curve $C$ as being traced out in time by vector $\vec x$, which is a function of parameter $t$: $\vec x = g(t)$. So $C$ is a trajectory we're following with $g(t)$.
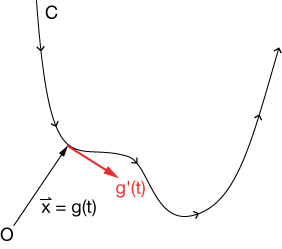
We know that if we take the derivative of that parametric function, $g'(t)$, that the resulting vector (
$$\frac{\partial F}{\partial x} \frac{dx}{dt} + \frac{\partial F}{\partial y} \frac{dy}{dt} + \frac{\partial F}{\partial z} \frac{dz}{dt} = 0$$
which is
$$\nabla F \cdot \frac{d \vec x}{dt} = 0$$
This means that the dot product of the gradient of $F$ with $\frac{dx}{dt}$ is zero, so $\nabla F$ ust be normal to $\frac{dx}{dt}$
Example 3
Let's revisit our first example, the sphere $x^2 + y^2 + z^2 = 9$, and find the plane tangent to it at $(1, 2, 2)$ using the gradient method.
$$ \begin{align} F_x &= 2x \phantom{00} \rightarrow \phantom{00} F_x(1,2,2) = 2 \\[5pt] F_y &= 2y \phantom{00} \rightarrow \phantom{00} F_y(1,2,2) = 4 \\[5pt] F_z &= 2z \phantom{00} \rightarrow \phantom{00} F_z(1,2,2) = 4 \\[5pt] \end{align}$$
So $\vec n = \nabla F(1, 2, 2) = (2, 4, 4)$
Then the equation of our plane is
$$ \begin{align} 2(x-1) + 4(y-2) + 4(z-2) &= 0 \\[5pt] 2x - 2 + 4y - 8 + 4z - 8 &= 0\\[5pt] 2x + 4y + 4z &= 18 \\[5pt] x + 2y + 2z &= 9 \end{align}$$
This is identical to the result we got above.
Practice problems
Find an equation of the plane tangent to the surface at the given point.
-
$z = 5 - 2x^2 - y^2 \; \text{ at } \; (1, -1, 2)$
Solution
First we'll write $F = 5 - 2x^2 - y^2 - z = 0$. Then calculate the partial derivatives:
$$ \begin{align} F_x &= -4x \phantom{00} \rightarrow \phantom{00} F_x(1,-1,2) = -4 \\[5pt] F_y &= -2y \phantom{00} \rightarrow \phantom{00} F_y(1,-1,2) = 2 \\[5pt] F_z &= -1 \phantom{00} \rightarrow \phantom{00} F_z(1,-1,2) = -1 \end{align}$$
So $\vec n = \nabla F(1, -1, 2) = (-4,2,-1)$
Then the equation of our plane is
$$ \begin{align} -4(x-1) + 2(y+1) -1(z-2) &= 0 \\[5pt] -4x + 4 + 2y + 2 -z +2 &= 0\\[5pt] -4x + 2y - z &= -8 \\[5pt] 4x - 2y + z &= 8 \end{align}$$
-
$x^2 + y^2 + 2z^2 = 9 \; \text{ at } \; (1, 0, 2)$
Solution
First we'll write $F = x^2 + y^2 + 2z^2 - 9 = 0$. Then calculate the partial derivatives:
$$ \begin{align} F_x &= 2x \phantom{00} \rightarrow \phantom{00} F_x(1,0,2) = 2 \\[5pt] F_y &= 2y \phantom{00} \rightarrow \phantom{00} F_y(1,0,2) = 0 \\[5pt] F_z &= 4 \phantom{00} \rightarrow \phantom{00} F_z(1,0,2) = 8 \end{align}$$
So $\vec n = \nabla F(1,0,2) = (2,0,8)$
Then the equation of our plane is
$$ \require{cancel} \begin{align} 2(x-1) + \cancel{0(y-0)} + 8(z-2) &= 0 \\[5pt] 2x - 2 + 8z - 16 &= 0\\[5pt] 2x + 8z &= 18 \\[5pt] x + 4z &= 9 \end{align}$$
-
$x^2 + 2y^2 + 3z^2 = 6 \; \text{ at } \; (1, -1, 1)$
Solution
First we'll write $F = x^2 + 2y^2 + 23z^2 - 6 = 0$. Then calculate the partial derivatives:
$$ \begin{align} F_x &= 2x \phantom{00} \rightarrow \phantom{00} F_x(1,-1,1) = 2 \\[5pt] F_y &= 4y \phantom{00} \rightarrow \phantom{00} F_y(1,-1,1) = -4 \\[5pt] F_z &= 6z \phantom{00} \rightarrow \phantom{00} F_z(1,-1,1) = 6 \end{align}$$
So $\vec n = \nabla F(1,-1,1) = (2,-4,6)$
Then the equation of our plane is
$$ \require{cancel} \begin{align} 2(x-1) - 4(y+1) + 6(z-1) &= 0 \\[5pt] 2x - 2 -4y -4 + 6z -6 &= 0\\[5pt] 2x -4y + 6z &= 12 \\[5pt] x - 2y + 3z &= 6 \end{align}$$
-
$xyz = 24 \; \text{ at } \; (2, 3, 4)$
Solution
First we'll write $F = xyz - 24 = 0$. Then calculate the partial derivatives:
$$ \begin{align} F_x &= yz \phantom{00} \rightarrow \phantom{00} F_x(2,3,4) = 12 \\[5pt] F_y &= xz \phantom{00} \rightarrow \phantom{00} F_y(2,3,4) = 8 \\[5pt] F_z &= xy \phantom{00} \rightarrow \phantom{00} F_z(2,3,4) = 6 \end{align}$$
So $\vec n = \nabla F(2,3,4) = (12,8,6)$
Then the equation of our plane is
$$ \require{cancel} \begin{align} 6(x-2) + 8(y-3) + 6(z-4) &= 0 \\[5pt] 6x - 12 + 8y - 24 + 6z - 24 &= 0\\[5pt] 6x + 8y + 6z &= 60 \\[5pt] 3x + 4y + 3z &= 30 \end{align}$$
Suppose we have a 3-D surface traced by a vector function
$$\vec r = x(u,v) \, \hat i + y(u,v) \, \hat j + z(u,v) \, \hat k$$
Here's the setup for finding the equation of the tangent plane:
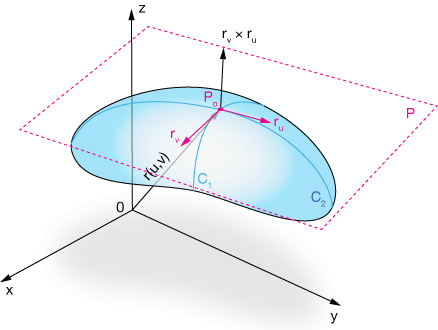
Any point on the surface is given by vector $vec r(u,v)$, where $u$ and $v$ arhe the parameters Coordinates $x, \; y$ and $z$ are all functions of $u$ and $v$. We can find the partial derivatives of $\vec r$ in the $u$ and $v$ directions at point $P_o$ like this:
$$ \begin{align} \vec r_u &= \frac{\partial x}{\partial u}(u_o,v_o) \, \hat i + \frac{\partial y}{\partial u}(u_o,v_o) \, \hat j+ \frac{\partial z}{\partial u}(u_o,v_o) \, \hat k \\[5pt] \vec r_v &= \frac{\partial x}{\partial v}(u_o,v_o) \, \hat i + \frac{\partial y}{\partial v}(u_o,v_o) \, \hat j+ \frac{\partial z}{\partial v}(u_o,v_o) \, \hat k \end{align}$$
Now $\vec r_u$ and $\vec r_v$ define our plane, $P$. Finally, the vector $\vec r_v \times \vec r_u$ is perpendicular to the plane, giving us enough information to find its equation.
In the figure, curves $C_1$ and $C_2$ are what we find when we hold one of the parameters constant and compute the partial derivatives in terms of the other.
Example 4
Determine the equation of the plane tangent to the surface with parametric equations $x = u^2, \; y = u+v, \; z = v^2$ at the point $P_o = (1, 2, 1)$.
$$ \begin{align} \vec r_u &= \frac{\partial u^2}{\partial u} \, \hat i + \frac{\partial (u+v)}{\partial u} \, \hat j+ \frac{\partial v^2}{\partial u} \, \hat k \\[5pt] &= 2u \, \hat i + \hat j \\[5pt] \vec r_v &= \frac{\partial u^2}{\partial v} \, \hat i + \frac{\partial (u+v)}{\partial v} \, \hat j+ \frac{\partial v^2}{\partial v} \, \hat k \\[5pt] &= \hat j + 2v \, \hat k \end{align}$$
The cross product $\vec r_u \times \vec r_v$ is
$$\vec r_u \times \vec r_v = \text{det} \left( \begin{matrix} \hat i & \hat j & \hat k \\ 2u & 1 & 0 \\ 0 & 1 & 2v \end{matrix} \right) = 2v \, \hat i + 2u \, \hat k - 4uv \, \hat j$$
Notice that to obtain the surface point $(1, 2, 1)$ we must have $u=1$ and $v=1$. So our cross product is $\vec r_u \times \vec r_v = 2 \, \hat i - 4 \, \hat j + 1 \, \hat k$.
Thus an equation of our tangent plane at $(1,2,1)$ is
$$ \begin{align} 2(x-1) -4(y-2) +1(z-1) &= 0 \\[5pt] 2x - 2 -4y +8 +z-1 &= 0 \\[5pt] 2x - 4y + z &= -5 \end{align}$$

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2024-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.