Definition
The partial derivative of a function of more than one variable is its derivative with respect to one of those variables, holding the others constant. The partial derivative (sometimes "the partial") gives the slope of a function along one of its dimensions.
The notation is similar to the Leibniz notation for derivatives, but with a different-looking "d":
$$\frac{\partial f(x, y)}{\partial x}$$
is the derivative of the two dimensional function $f(x, y)$ taken with respect to the variable $x$, and holding the variable $y$ as a constant.
Sometimes partials (this time let's use a 3-D function) are written like this:
$$\left( \frac{\partial f}{\partial x} \right)_{y, z}$$
means the derivative of the function $f(x, y, z)$ with respect to $x$, holding the variables $y$ and $z$ constant.
A quick example
Consider the two-variable function $f(x, y) = 4x^3 + 3x^2y - 2xy^2 + y^3$.
(a) Find the partial derivative of $f$ with respect to $x$.
Here we treat the variable $y$ as a constant and find $\frac{df}{dx}$
$$\frac{\partial f(x, y)}{\partial x} = 12x^2 + 6xy - 2y^2$$
(b) Find the partial derivative of $f$ with respect to $y$.
Here we treat the vaiable $x$ as a constant and find $\frac{df}{dy}$
$$\frac{\partial f(x, y)}{\partial y} = 3x^2 - 4xy + 3y^2$$
Pro tip: getting the hang of it
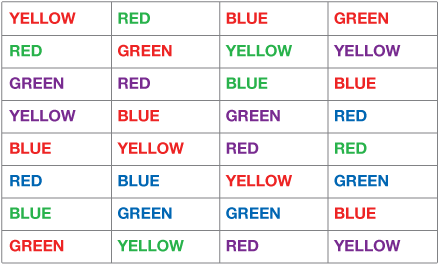
Here's a little exercise that can show you what it can sometimes be like to find a proper partial derivative. Try reading the words in the table, first as written words — ignoring the color, then run back through it, but instead of reading the words, say the color of the word out loud. It's trickier than you might think.
That's the trick to finding partials: focusing on the variable of interest and just treating the other(s) as though they were numbers. You'll get the hang of it.
Derivation
Consider a function of two variables, $f(x, y)$, and let $(x, y)$ be a point in the domain of $f(x, y)$. Then
$$ \begin{align} \frac{\partial f(x,y)}{\partial x} = \lim_{h \rightarrow 0} \frac{f(x + h, y) - f(x, y)}{h} \\[8pt] \frac{\partial f(x,y)}{\partial y} = \lim_{k \rightarrow 0} \frac{f(x, y + k) - f(x, y)}{k} \end{align}$$
as long as that limit exists. This is just how we developed the derivative for a function of a single variable.
In more general terms, the partial derivatives of a function of an $n$-dimensional vector $\vec a$
We define $f(\vec a) = f(a_1, a_2, \dots , a_n)$, where $\vec a$ is an $n$-dimensional vector. Then we define the partial derivative of $f$ with respect to the $i^{th}$ independent variable, $x_i$ as
$$ \begin{align}\frac{\partial f(\vec a)}{\partial x_i} &= \lim_{h \rightarrow 0} \frac{f(a_1, a_2, \dots, a_{i-1}, a_i + h, a_{i+1}, \dots , a_n) - f(a_1, a_2, \dots, a_i, \dots, a_n)}{h} \\[5pt] &= \lim_{h \rightarrow 0} \frac{f(\vec a + h\vec{e}_i)- f(\vec a)}{h} \end{align}$$
In the last expression, the vector $\vec {e}_i$ is the unit vector in the direction of our variable $x_i$. for example, for a three-variable equation in which our function $f$ is a function of the 3D vector $\vec a = (x_1, x_2, x_3)$, and we're taking the partial derivative with respect to $x_3$, $\vec{e}_3 = (0, 0, 1)$. It's just a fancy way of selecting the variable for which we're finding the slope of this function.
Example 1
Find and interpret the partial derivatives of $z = 2x^2-3y^2 + 4$.
The graph of this function is shown below. It has a saddle point at $(0, 0, 4)$
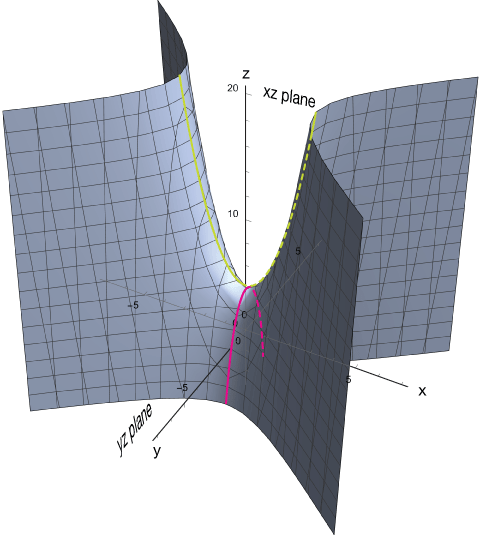
The slice of this function along the $xz$ plane is found by setting $y = 0$:
$$ \begin{align} z &= 2x^2-3y^2+4 \\[5pt] z &= 2x^2 + 4 \end{align}$$
which is an upward-opening parabola with vertex $(0, 4)$ in the $xz$ plane. We know the derivative of this function with respect to $x$:
$$\frac{dz}{dx} = 4x$$
A tangent to this surface in the $xz$ plane is the line $z = 4x$. Likewise, if we slice this graph in the $yz$ plane, the function $z = -6y$ gives the slope of a downward-opening parabola centered at $(0, 4)$
The partial derivatives are
$$ \begin{align} \frac{\partial z}{\partial x} &= 4x \\[5pt] \frac{\partial z}{\partial y} &= -6y, \end{align}$$
just what we'd expect.
Example
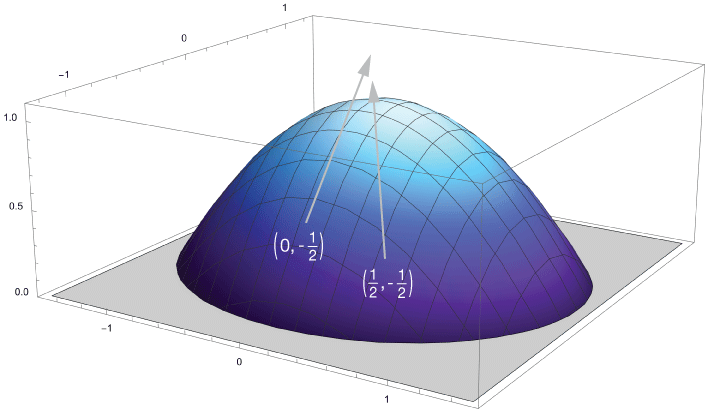
Calculate the gradient of the 3D function $f(x, y) = 1 - \frac{1}{2} x^2 - y^2$.
$$ \begin{align} \nabla f(x, y) &= \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right) \\[5pt] &= (-x, -2y) \end{align}$$
In the graph below, the unit vectors for the direction of the gradients at $(0, -\frac{1}{2})$ and $(\frac{1}{2}, -\frac{1}{2})$ are shown.
Here's a top view of that paraboloid showing the same unit vectors marking those gradients vectors. You're looking down into that "box," along the z-axis.
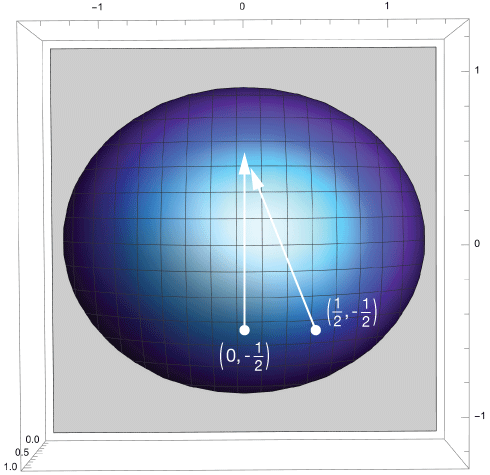
Below is a full map of the gradient vectors on a grid of representative points. It's a lot like a contour map with which you might climb a mountain.
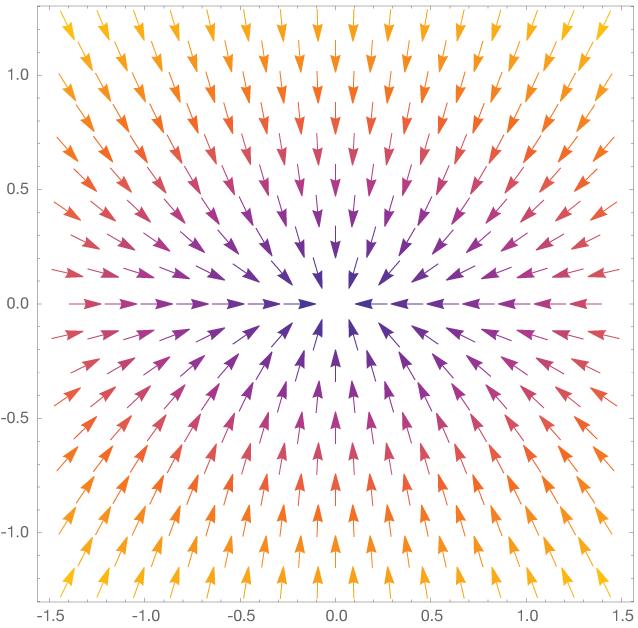
Practice problems
Consider the multidimensional functions below. For 3D functions (functions of $x$ and $y$), findl $\frac{\partial f(x,y)}{\partial x}$ and $\frac{\partial f(x,y)}{\partial y}$. For 4D functions (functions of $x$, $y$ and $z$) find the partial derivative with respect to $z$ as well.
-
$f(x, y) = x^4 y^3 - 7 x^2 y - y^4 + 5x$
Solution
$$ \begin{align} \frac{\partial f}{\partial x} &= 4x^3 y^3 - 14 xy + 5 \\[5pt] \frac{\partial f}{\partial y} &= 3x^4 y^2 - 7x^2 - 4y^3 \end{align}$$
-
$f(x, y) = (x^2 + y^3)^9 + 2ln(x)$
Solution
$$ \begin{align} \frac{\partial f}{\partial x} &= 9(x^2 + y^3)^8 (2x) + \frac{2}{x} \\[5pt] &= 18(x^2 + y^3)^8 + \frac{2}{x} \\[5pt] \frac{\partial f}{\partial y} &= 9(x^2 + y^3)^8 (3y^2) \\[5pt] &= 27 y^2 (x^2 + y^3)^8 \end{align}$$
-
$f(x, y) = x e^{xy}$
Solution
$$ \begin{align} \frac{\partial f}{\partial x} &= e^{xy} + x e^{xy}(y) = e^{xy}(1 + xy) \\[5pt] \frac{\partial f}{\partial y} &= xe^{xy} (x) = x^2 e^{xy} \end{align}$$
-
$f(x, y, z) = \frac{x}{x+y+z}$
Solution
$$ \begin{align} \frac{\partial f}{\partial x} &= \frac{(x+y+z)(1) - x(1)}{(x+y+z)^2} \\[5pt] &= \frac{y + z}{(x+y+z)^2} \\[5pt] \frac{\partial f}{\partial y} &= \frac{0 - x(1)}{(x+y+z)^2} - \frac{-x}{(x+y+z)^2}\\[5pt] \frac{\partial f}{\partial z} &= \frac{0 - x(1)}{(x+y+z)^2} - \frac{-x}{(x+y+z)^2} \end{align}$$
Here we've used the quotient rule for all derivatives
-
$f(x, y) = \frac{6x^2 + 2xy}{3y^2 - x^2}$
Solution
$$ \begin{align} \frac{\partial f}{\partial x} &= \frac{(3y^2 - x^2)(12x + 2y)-(6x^2 + 2xy)(-2x)}{(3y^2 - x^2)^2} \\[5pt] \frac{\partial f}{\partial y} &= \frac{(3y^2-x^2)(2x)-(6x^2+2xy)(6y)}{(3y^2-x^2)^2} \end{align}$$
Here we've used the quotient rule for all derivatives
-
$f(x, y) = \frac{\text{sin}(y)}{3x^2}$
Solution
$$ \begin{align} \frac{\partial f}{\partial x} &= \frac{3x^2(0) - sin(y)(6x)}{9x^4} = \frac{-6 sin(y)}{9x^3} \\[5pt] \frac{\partial f}{\partial y} &= \frac{1}{3x^2} cos(y) \end{align}$$
Here we've used the quotient rule for all derivatives
-
$f(x, y, z) = xy \cdot cos(xyz)$
Solution
$$ \begin{align} \frac{\partial f}{\partial x} &= y \, cos(xyz) - xy \, sin(xyz) (yz) \\[5pt] &= y \, cos(xyz) - xy^2z \, sin(xyz) \\[5pt] \frac{\partial f}{\partial y} &= x \, cos(xyz - xy \, sin (xyz) (xz)\\[5pt] &= x \, cos(xyz) - x^2yz \, sin(xyz) \\[5pt] \frac{\partial f}{\partial z} &= -xy \, sin(xyz)(xy) \\[5pt] &= x^2 y^2 \, sin(xyz) \end{align}$$
-
$f(x, y) = \text{sin}(xy) + 3xy$
Solution
$$ \begin{align} \frac{\partial f}{\partial x} &= \text{cos}(xy)(y) + 3y = y(\text{cos}(xy)+3) \\[5pt] \frac{\partial f}{\partial y} &= \text{cos}(xy)(x) + 3x = x(\text{cos}(xy)+3) \end{align}$$
Second partials
We can also find partial second derivatives of multivariable or vector functions. The notation of the second partial derivatives of $f(x, y)$ with respect to $x$ and $y$ are
$$\frac{\partial^2 f}{\partial x^2} \phantom{000} \text{ and } \phantom{000} \frac{\partial^2 f}{\partial y^2}$$
Some other notations are reviewed in the box below.
Example
Here's an example of some partial second derivatives of the function $f(x, y) = x^3 y^2 - y^4 x$.
$$ \begin{align} \frac{\partial^2 f}{\partial x^2} &= \frac{\partial}{\partial x} (3x^2 y^2 - y^4) \\[5pt] &= 6x y^2 \\[5pt] \frac{\partial^2 f}{\partial y^2} &= \frac{\partial}{\partial y} (2y x^3 - 4y^3) \\[5pt] &= 2x^3 - 12 y^2 x \end{align}$$
The
Mixed partials
The
$$\frac{\partial f(x,y)}{\partial x \partial y}$$
The Gradient, $\nabla$
The gradient of a multidimensional function is a vector function that gives the direction of the fastest increase in slope (steepest slope). It is found by taking the partial derivative of the function with respect to each component of the vector.
The gradient is given the symbol $\nabla$, which is called "nabla", but is often referred to as "del". So when someone says "calculate del $f$," they mean "calculate the gradient of the function $f$."
$$\nabla f(x_1, x_2, \dots x_n) = \left( \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \dots, \frac{\partial f}{\partial x_n} \right)$$
Here's a quick example. Let's take the 3D function
$$f(x, y) = yx^2 + 2xy$$
and find the gradient:
$$ \begin{align} \nabla f(x, y) &= (2xy + 2y, \; x^2 + 2x) \\[5pt] &= \langle 2y(x + 1), \; x(x + 2) \rangle \end{align}$$
That set of vectors gives the direction of the steepest slope anywhere on $f(x, y)$.
The figure below is a plot of our function with two (normalized) gradient vectors drawn in at points $(3, -3)$ and $(4, 4)$.
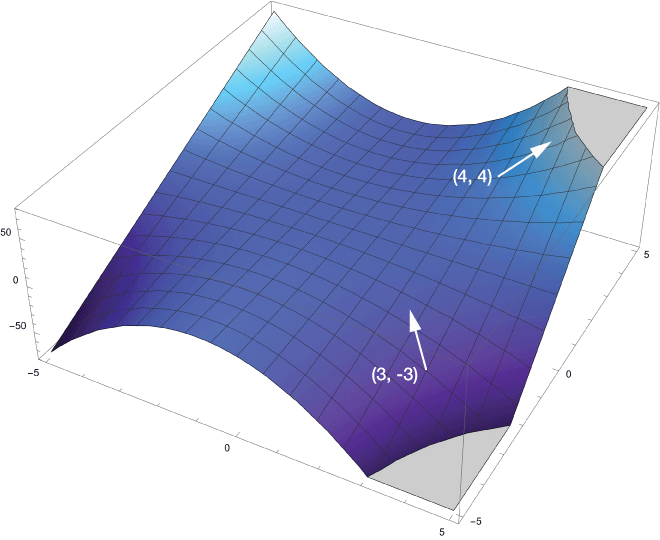

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2016-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.

