Linear geometry in $\mathbb{R}^3$
On this page we'll use our knowledge of vectors to determine the equations of lines and planes in 3-D space.
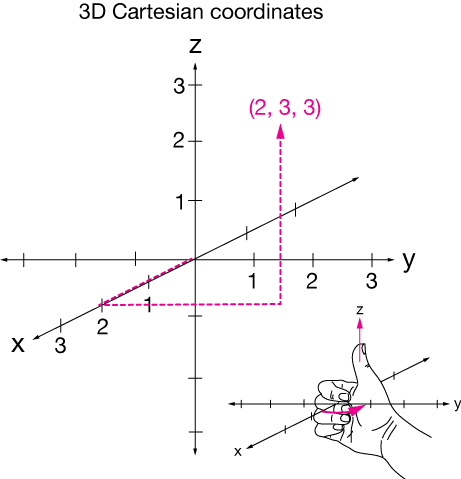
In all of what follows, we'll be using a right-handed 3-dimensional Cartesian coordinate system like the one shown here. "Right-handed" in this sense means that if we trace the direction of the positive end of the $x$-axis as it rotates toward the positive end of the $y$-axis with the fingers of our right hand, our right thumb must point in the positive direction of the $z$-axis. (If you did this with your left hand, $z$ would point downward. The same would be true if you switched the $x$ and $y$ axes and used your right hand.) Take a minute to make sure you can visualize the plotting of points on such a coordinate system. It's not always easy, but the more effort you put into it, the better you'll get at it.
One point, $(x, y, z) = (2, 3, 3)$ is shown. To locate the point, we move 2 units toward us (out of the plane of the screen), then 3 units right and 3 units upward.
Vectors – a refresher
A vector is a directed line segment that can be used to represent some physical quantity like velocity or force, or that can be used to point to a specific location in some n-dimensional space, where n can be anything larger than 1. A one-dimensional vector is a scalar, a number without direction.
The only two important properties of a vector are its length and its direction. In the graph below, the 2-D vector $\vec{A}$ is written in several locations on the plane. Each version represents the same vector because the length and direction is preserved; its location is irrelevant.
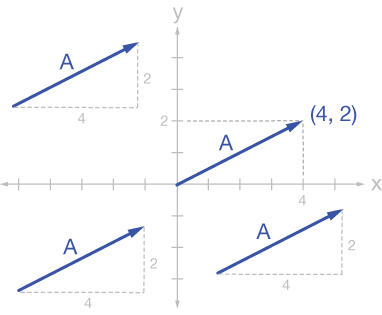
Any vector can be labeled with a set of coordinates, like the $\langle 4, 2\rangle $ on the graph. It's easy to find the coordinates of a vector when its origin (the non-pointed end) is at the graph origin. No matter where the vector is located, however, we can simply mentally translate the origin of the axis system to the start of the vector (non-arrow end) and count along the axes to find the same coordinates.
The length or magnitude of a two-dimensional vector can be found using the Pythagorean theorem. The length of vector $\langle 2, 4 \rangle $ in the figure is
$$ \begin{align} L &= \sqrt{x^2 + y^2} \\[5pt] &= \sqrt{2^2 + 4^2} = \sqrt{20} \\[5pt] &= 2 \sqrt{5} \end{align}$$
This formula for the length of a vector can be generalized to vectors of any number of dimensions. The length of an $n$-dimensional vector, $(v_1, v_2, \dots , v_n)$ is
$$L = \sqrt{n_1^2 + n_2^2 + \dots + n_n^2}$$
Normalizing vectors
To normalize a vector means to keep its direction, but reduce its length to one, which we call unit length. This is done by dividing each coordinate of the vector by its length. Here's an example. Let's normalize the vector $\vec{v} = \langle 2, -1, 3\rangle.$
First we find the length of $\vec{v}:$
$$ \begin{align} L &= \sqrt{2^2 + (-1)^2 + 3^2} \\[5pt] &= \sqrt{4 + 1 + 9} \\[5pt] &= \sqrt{14} \end{align}$$
Now the normalized version of $\vec{v}$ is
$$\hat{v} = \bigg< \frac{2}{\sqrt{14}}, \frac{-1}{\sqrt{14}}, \frac{3}{\sqrt{14}} \bigg>$$
Notice that, once normalized, we wrote the vector using the "hat" symbol, $\hat{v},$ which we reserve for unit vectors. You can check that the length of this vector is one.
This normalization process can be used on vectors of any dimension.
A handy feature of normalization is that if we want a vector in the same direction but of length 3, it's just $3 \hat v$.
Adding vectors
Geometrically, we add two vectors by joining them in "head-to-tail" fashion. Here's a picture of the addition of two 2-D vectors.
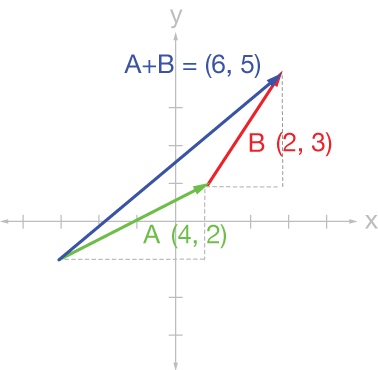
In the graph we add two vectors, $\vec A$ and $\vec B$ graphically. The blue vector is the resultant, the sum of the two. Numerically, we simply add the $x$ and $y$ coordinates to get the coordinates of the sum vector: $(4+2, \; 2+3) = (6, \, 5)$.
The sum of two n-dimensional vectors, $\vec{v_1} = \langle x_1, y_1, z_1\rangle$ and $\vec{v_2} = \langle x_2, y_2, z_2\rangle$ can be added by adding their respective terms:
$$\vec{v_1} + \vec{v_2} = \langle x_1 + x_2, y_1 + y_2, z_1 + z_2\rangle$$
Only vectors of the same dimension can be summed, but vector addition works the same way for any number of dimensions. Subtraction of one vector from another can be viewed as addition of the negative, where $-\vec{v}$ is the same as $\vec{v},$ but pointing in the opposite direction.
Adding a point, $(a, \; b, \; c)$ to a vector works the same way. It's just a translation of that vector so that it starts at $(a, \; b, \; c)$.
Practice problems
Add the two vectors to obtain $\vec{v},$ then normalize the resulting vector to obtain $\hat{v}.$
-
$\vec{v} = \langle -2, 2, 3\rangle + \langle 2, -4, 5\rangle$
Solution
$$S = \langle -2 + 2, 2 - 4, 3 + 5\rangle = \langle 0, -2, 8\rangle $$
$$ \begin{align} \text{length} &= \sqrt{0^2 + (-2)^2 + 8^2} \\[5pt] &= \sqrt{4 + 64} = \sqrt{68} \\[5pt] &= 2 \sqrt{17} \end{align}$$
$$\hat{v} = \bigg< 0, \frac{-1}{\sqrt{17}}, \frac{4}{\sqrt{17}} \bigg> $$
-
$\vec{v} = \langle 1, 4, -4\rangle + \langle 2, -3, 7\rangle$
Solution
$$S = \langle 1 + 2, 4 - 3, -4 + 7\rangle = \langle 3, 1, 3\rangle $$
$$ \begin{align} \text{length} &= \sqrt{3^2 + 1^2 + 3^2} \\[5pt] &= \sqrt{9 + 1 + 9} = \sqrt{19} \end{align}$$
$$\hat{v} = \bigg< \frac{3}{\sqrt{19}}, \frac{1}{\sqrt{19}}, \frac{3}{\sqrt{19}} \bigg> $$
-
$\vec{v} = (-3, 4, -3) - (2, 2, -1)$
Solution
$$S = (-3 + 2, 4 + 2, -3 - 1) = (-1, 6, -4)$$
$$ \begin{align} \text{length} &= \sqrt{(-1)^2 + 6^2 + (-4)^2} \\[5pt] &= \sqrt{1 + 36 + 16} = \sqrt{53} \end{align}$$
$$\hat{v} = \left( \frac{-1}{\sqrt{53}}, \frac{6}{\sqrt{53}}, \frac{-4}{\sqrt{53}} \right)$$
-
$\vec{v} = (1, -2, -4, 3) + (2, -2, 1, -4)$
Solution
$$ \begin{align} S &= (1 + 2, -2 - 2, -4 + 1, 3 - 4) \\[5pt] &= (3, -4, -3, -1) \end{align}$$
$$ \begin{align} \text{length} &= \sqrt{3^2 + (-4)^2 + (-3)^2 + (-1)^2} \\[5pt] &= \sqrt{9 + 16 + 9 + 1} = \sqrt{35} \end{align}$$
$$\hat{v} = \left( \frac{3}{\sqrt{35}}, \frac{-4}{\sqrt{35}}, \frac{-3}{\sqrt{35}}, \frac{-1}{\sqrt{35}} \right)$$
3-D unit vectors: $\hat{i}, \; \hat{j}, \; \hat{k}$
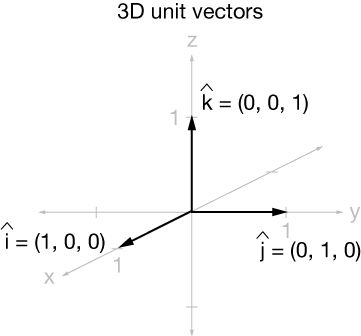
Before we begin talking about multidimensional vectors in earnest, let's talk about the three Cartesian basis vectors, $\hat{i}, \; \hat{j}, \; \hat{k}.$ They are
$$ \begin{align} \hat{i} &= (1, 0, 0) \\[5pt] \hat{j} &= (0, 1, 0) \\[5pt] \hat{k} &= (0, 0, 1) \end{align}$$
Using unit vectors
Let's express the 3-D vector $(-3, 4, 8)$ in terms of the unit vectors:
$$ \begin{align} (-3, 4, 8) &= -3(1, 0, 0) + 4((0, 1, 0) + 8(0, 0, 1) \\[5pt] &= -3 \hat{i} + 4 \hat{j} + 8 \hat{k} \end{align}$$
Using unit vectors
The 3-D unit vectors form a basis for 3-D space. Any vector $(a, b, c)$ can be written as a sum of parameters multiplied by each basis vector:
$$ \begin{align} \langle a, b, c\rangle &= a\langle 1, 0, 0\rangle + b \langle 0, 1, 0\rangle + c\langle 0, 0, 1\rangle \\[5pt] &= a \hat{i} + b \hat{j} + c \hat{k} \end{align}$$
Pro tip 1: Often unit vectors like $\hat{i}$ are referred to as "i hat" because the symbol $\hat{}$ looks like a hat.
Pro tip 2: In higher dimensional systems, we usually use the letter $e$ to denote the set of unit vectors. In an $n$-dimensional coordinate system, the unit vectors are $e = \{\hat e_1, \hat e_2, \dots , \hat e_n \}$.
Equations of lines
Just as the equation of a line in a plane can be determined using a point and the slope of the line, we can determine the equation of a line in 3-D space. To do so we need a single point and a vector pointing in the same direction as the line.
The setup looks like this:
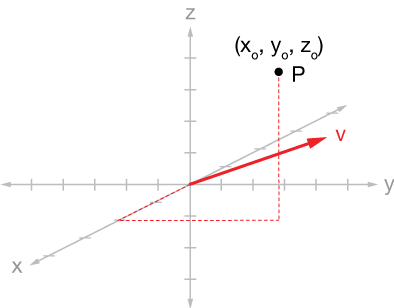
We have a point, $P = (x_o, \; y_o, \; z_o),$ and a direction vector $\vec{v}$ and we will draw the vector $\vec r_o = \langle x_o, \; y_o, \; z_o\rangle$ to point $P$, as shown in the second graph.
Now because two points define a line, let's imagine a second point $Q = (x, y, z)$ on our line. Then the vector from $Q$ to $P$, $\overrightarrow{QP},$ is
$$\vec Q - \vec{P} = \langle x - x_0, \; y - y_0, \; z - z_0 \rangle $$
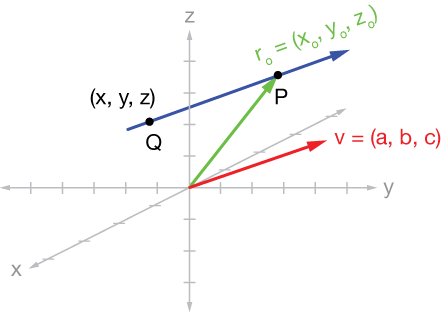
We've also labeled the coordinates of vector $\vec{v}$ as $\vec{v} = \langle a, \; b, \; c\rangle$.
Now if $\overrightarrow{QP}$ is parallel to our direction vector $\vec r_0 ,$ then the two differ by only a constant or parameter, $t.$
$$\overrightarrow{QP} = t \vec{v}.$$
If the coordinates of vector $\vec{r_0}$ are $\langle a, b, c\rangle,$ then the equation of our line is
$$\langle x, y, z\rangle - \langle x_0, y_0, z_0\rangle = t \cdot \langle a, b, c\rangle $$
We can rearrange to
$$ \begin{align} \langle x, y, z\rangle &= \langle x_0, y_0, z_0\rangle + t\langle a, b, c\rangle \\[5pt] \phantom{000} \vec{r} \phantom{000} &= \phantom{000} \vec{r_0} \phantom{000} + \phantom{000} t \vec{v} \end{align}$$
This is analogous to the equation for a line in the x-y plane, $y = mx + b,$ where y is the dependent variable, $m$ is the slope and $b$ is a point on the line, a specific one in this case, the y-axis intercept, but nonetheless, just a point. By analogy in the equation $\vec{r} = \vec{r_0} + t \vec{v},$ we have the variable vector $\vec{r}$ as our independent variable, the point $(x_0, y_0, z_0)$ as our fixed, known point, and vector $\vec{v} = \langle a, b, c\rangle $ is our slope.
We can break this equation up into three parametric equations:
$$ \begin{align} x &= x_0 + ta \\[5pt] y &= y_0 + tb \\[5pt] z &= z_0 + tc \end{align}$$
Finally, we can express the equation of the line in parametric form like this:
$$(x, y, z) = (x_0 + ta, y_0 + tb, z_0 + tc)$$
Now let's do a couple of examples to see how this all comes together in practice.
Example 1
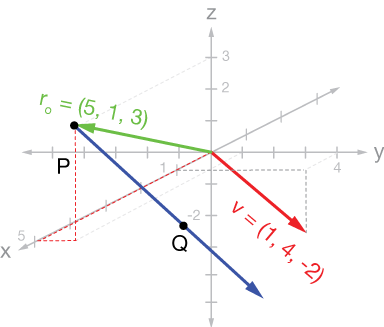
Find the vector equation of the line passing through $P = (5, 1, 3)$ and parallel to (or in the direction of) the vector $\vec{v} = \hat{i} + 4 \hat{j} - 2 \hat{k}.$
$$(x, y, z) = (x_0, \; y_0, \; z_0) + t \cdot \langle a, \; b, \; c\rangle,$$
where
$$ \begin{align} (x_0, \; y_0, \; z_0) &= (5, \; 1, \; 3) \\[5pt] \langle a, \; b, \;c\rangle &= \langle 1, \; 4, -2\rangle \end{align}$$
So our equation is
$$(x, y, z) = (5, 1, 3) + t\langle 1, 4, -2\rangle $$
We can write this as a list of parametric equations:
$$ \begin{align} x &= 5 + t \\[5pt] y &= 1 + 4t \\[5pt] z &= 3 - 2t \end{align}$$
or as a parameterized vector:
$$(x, y, z) = (5 + t, 1 + 4t, 3 - 2t)$$
Example 2
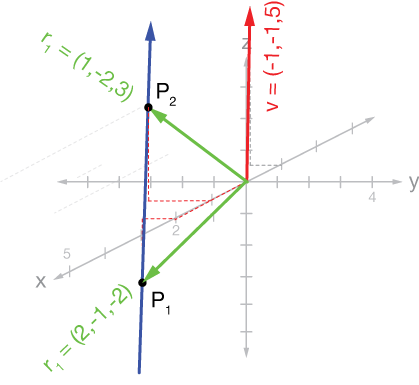
Find the vector equation of the line passing through points $P_1 = (2, -1, -2)$ and $P_2 = (1, -2, 3).$
$$ \begin{align} P_2 - P_1 &= (1, -2, 3) - (2, -1, -2) \\[5pt] &= \langle 1 - 2, -2 - (-1), 3 - (-2)\rangle \\[5pt] &= \langle -1, -1, 5\rangle \end{align}$$
So our direction vector is $\vec{r_0} = \langle -1, -1, 5\rangle.$
The initial equation of our line is then
$$(x, y, z) = (2, -1, -2) + t\langle -1, -1, 5\rangle $$
The parametric equations are:
$$ \begin{align} x &= 2 - t \\[5pt] y &= -1 - t \\[5pt] z &= -2 + 5t \end{align}$$
and the parameterized vector is
$$(x, y, z) = (2 - t, -1 - t, -2 + 5t)$$
Practice problems
Find an equation of the line passing through the point and parallel to the given vector
-
$(-2, 2, 3)$ parallel to $\hat{i} - \hat{j} + 2 \hat{k}$
Solution
$$ \begin{align} (x, y, z) &= (-2, 2, 3) + t(1, -1, 2) \\[5pt] &= (-2 + t, 2 - t, 3 + 2t) \end{align}$$
-
$(1, 3, 3)$ parallel to $2\hat{i} + \hat{j} - \hat{k}$
Solution
$$ \begin{align} (x, y, z) &= (1, 3, 3) + t(2, 1, -1) \\[5pt] &= (1 + 2t, 3 + t, 3 - t) \end{align}$$
-
$(1, 4, -3)$ parallel to $-2\hat{i} - 3\hat{j} + \hat{k}$
Solution
$$ \begin{align} (x, y, z) &= (1, 4, -3) + t(-2, -3, 1) \\[5pt] &= (1 - 2t, 4 - 3t, -3 + t) \end{align}$$
-
$(1, 1, -4)$ parallel to $-\hat{i} - \hat{j} + 2\hat{k}$
Solution
$$ \begin{align} (x, y, z) &= (1, 1, -4) + t(-1, -1, 2) \\[5pt] &= (1 - t, 1 - t, -4 + 2t) \end{align}$$
Find an equation of the line passing through the points given.
-
$(-2, 2, -1)$ and $(-2, -3, 1)$
Solution
point: $(-2, 2, -1),$ direction:
$$ \begin{align} \vec{v} &= (-2 - (-2), 2 - (-3), -1 - 1) \\[5pt] &= (0, 5, -2) \end{align}$$
$$ \begin{align} (x, y, z) &= (-2, 2, -1) + t(0, 5, -2) \\[5pt] &= (-2, 2 + 5t, -1 -2t) \end{align}$$
-
$(4, 2, 5)$ and $(-1, -1, -1)$
Solution
point: $(4, 2, 5),$ direction:
$$ \begin{align} \vec{v} &= (4 - (-1), 2 - (-1), 5-(-1)) \\[5pt] &= (5, 3, 6) \end{align}$$
$$ \begin{align} (x, y, z) &= (4, 2, 5) + t(5, 3, 6) \\[5pt] &= (4 + 5t, 2 + 3t, 5 + 6t) \end{align}$$
-
$(-3, 4, -3)$ and $(2, 2, -1)$
Solution
point: $(2, 2, -1),$ direction:
$$ \begin{align} \vec{v} &= (2 - (-3), 2 - 4, -1 - (-3)) \\[5pt] &= (5, -2, 2) \end{align}$$
$$ \begin{align} (x, y, z) &= (2, 2, -1) + t(5, -2, 2) \\[5pt] &= (2 + 5t, 2 - 2t, -1 + 2t) \end{align}$$
-
$(3, 4, -1)$ and $(-1, -2, 4)$
Solution
point: $(3, 4, -1),$ direction:
$$ \begin{align} \vec{v} &= (3 - (-1), 4 - (-2), -1 - 4) \\[5pt] &= (4, 6, -5) \end{align}$$
$$ \begin{align} (x, y, z) &= (3, 4, -1) + t(4, 6, -5) \\[5pt] &= (3 + 4t, 4 + 6t, -1 - 5t) \end{align}$$
Relationships between lines in $\mathbb{R}^3$
In $\mathbb{R}^2$ space (the Cartesian plane), we can determine whether lines are parallel, intersect or coincide:
- If two lines have the same slope, they are parallel.
- If they have the same slope and share a point, then they are the same line (they are coincident).
- If two lines have different slopes, they intersect at one and only one point.
Lines in 3-D space can be parallel in that the distance between them remains constant, but they can also not be parallel and never intersect. These are called skew lines.
We can perform some similar tests to determine the relationship(s) between two lines in space. We'll do that through some examples.
Example 3
Find the intersection, if there is one, between the lines $(2, 1, 0) + t(-1, -1, -1)$ and $(3, 0, 5) + t\langle 2, 0, 6\rangle$.
$$ \begin{align} (2, 1, 0) &+ s\langle -1, -1, -1\rangle \\[5pt] &= (2-s, 1-s, -s) \\[9pt] (3, 0, 5) &+ t\langle 2, 0, 6\rangle \\[5pt] &= (3+2t, 0, 5+6t) \end{align}$$
Then set corresponding terms of each vector equal:
$$ \begin{align} 2 - s &= 3 + 2t \\[5pt] 1 - s &= 0 \\[5pt] -s &= 5 + 6t \end{align}$$
Here we have three equations and two unknowns, so this is a solvable system. The second equation gives $s = 1$. Plugging that into the third gives $t = -1.$ We can confirm both solutions by plugging into the first: $2 - 1 = 3 + 2(-1),$ which is true.
So these lines intersect at $(1, \; 0, -1)$, the point we get when we set $s=1$ in the first line or $t=-1$ in the second.
By analogy with lines in a plane, if we'd obtained no solution, that would mean that the lines do not cross. If we'd obtained an infinite number of solutions, the lines would be coincident (the same).
Example 4
Determine whether the lines $(2s - 3, s - 1, s - 4)$ and $(t - 3, 3t, 5 - 2t)$ intersect.
$$ \begin{align} 2s - 3 &= t - 3 \\[5pt] s - 1 &= 3t \\[5pt] s - 4 &= 5 - 2t \end{align}$$
From the second and third equations, we get
$$ \begin{align} s &= 1 + 3t \\[5pt] s &= 9 - 2t, \end{align}$$
Thus we can eliminate s by the transitive property and solve
$$ \begin{align} 1 + 3t &= 9 - 2t \\[5pt] 5t &= 8 \\[5pt] t &= \frac{8}{5}. \end{align}$$
Subbing into the first equation gives
$$ \require{cancel} \begin{align} 2s - 3 &= \frac{8}{5} - 3 \\[5pt] 2s &= \frac{8}{5} \\[5pt] s &= \frac{4}{5} \end{align}$$
Now we should make sure these work in all three equations. Subbing $s$ and $t$ into the first equation gives:
$$ \begin{align} 2 \left( \frac{8}{5} \right) &= \frac{4}{5} \\[5pt] \frac{16}{5} &\ne \frac{4}{5} \end{align}$$
So that's a contradiction, indicating that these lines have no point in common; they are skew lines.
Example 5
Consider the parametric lines
$$ \begin{align} \vec r_1 &= \langle t, \; t-1, \; 2t+3 \rangle \\[5pt] \vec r_2 &= \langle 2s, \; 2s-1, \; 4s+3 \rangle \end{align}$$
Learn what you can from these two lines: How are they oriented with respect to each other? Do they intersect? If so, where?
$$ \begin{align} \vec r_1 &= (0, -1, \; 3) + t \langle 1, \; 1, \; 2 \rangle \\[5pt] \vec r_2 &= (0, -1, \; 3) + s \langle 2, \; 2, \; 4 \rangle \end{align}$$
These lines have the same starting point and the same direction (notice that $\langle 2, \; 2, \; 4 \rangle$ is just a scalar multiple of $\langle 1, \; 1, \; 2 \rangle$, so both lines have the same direction. You could see this more clearly if you normalized both. So they represent the same line.
We could look at this algebraically by making the equations:
$$ \begin{align} t &= 2s \\[5pt] t-1 &= 2s-2 \\[5pt] 2t+3 &= 4s+6 \end{align}$$
Plugging $2s$ in for $t$ in either the second or third equations gives us an equality. This, too, proves that these lines are the same.
Practice problems
-
Show that the parametric equations
$$ \begin{align} x &= 2s+1, \; y = s+2, \; z = s-2 \\[5pt] x &= 6t+1, \; y = 3t+2, \; z = 3t-2 \end{align}$$
represent the same line.
Solution
We can reconstruct the parametric vector equations of these lines like this:
$$ \begin{align} \vec r_1 &= (1, \; 2, -2) + s\langle 2, \; 1, \; 1 \rangle \\[5pt] \vec r_2 &= (1, \; 2, -2) + s\langle 6, \; 3, \; 3 \rangle \end{align}$$
We can see that the starting point of both lines is the point $P = (1, \; 2, -2)$, so both lines go through the same point. The direction vectors are actually multiples of one another: $\langle 6, \; 3, \; 3 \rangle = 3 \langle 2, \; 1, \; 1 \rangle$, so they both also point in the same direction. Thus, they are the same line. You can prove to yourself that the normalized versions of both direction vectors are the same.
-
Show that the direction vectors of the lines
$$ \begin{align} L_1: \; x &= 2t, \; y = t-3, \; z = 1-t \\[5pt] L_2: \; x &= s, \; y = s+1, \; z = 3s - 2 \end{align}$$
are perpendicular and determine whether the lines intersect.
Solution
We can use the parametric forms to get the vector equations for these lines:
$$ \begin{align} L_1: \; (0, -3, 1) + t\langle 2, 1, -1\rangle \\[5pt] L_2: \; (0, 1, -2) + s\langle 1, 1, 3\rangle \\[5pt] \end{align}$$
Now the dot product of the direction vectors (the ones multiplied by the parameters) is
$$ \langle 2, \; 1,-1 \rangle \cdot \langle 1,\; 1, \; 3 \rangle = 2 + 1 - 3 = 0$$
so the direction vectors are perpendicular. Now to see if the lines intersect, we equate the $x, y$ and $z$ components of each:
$$ \begin{align} 2t &= s \tag{1} \\[5pt] t-3 &= s+1 \tag{2} \\[5pt] 1-t &= 3s - 2 \tag{3} \\[5pt] \end{align}$$
Now if we substitute $s = 2t$ for $s$ in (2), we get $t = -4$, and thus $s = -8$. Substituting both of these into (3) gives
$$1-(-4) \ne 3(-8) - 2$$
So the directions are perpendicular, but the lines are on different planes, and are thus skew.
-
Determine whether the lines
$$ \begin{align} L_1: \; x &= 3t+3, \; y = t, \; z = t+3 \\[5pt] L_2: \; x &= s-2, \; y = 2s-5, \; z = s \end{align}$$
intersect
Solution
First equate the parametric versions of each of the $x, y$ and $z$ terms of each line:
$$ \begin{align} 3t + 3 &= s-2 \tag{1} \\[5pt] t &= 2s - 5 \tag{2} \\[5pt] t + 3 &= s \tag{3} \end{align}$$
If we solve (2) and (3) for $t$ and equate them, eliminating $t$, we get
$$ \begin{align} 2s - 5 &= s - 3 \\[5pt] s &= 2 \end{align}$$
Then using (2), we can find $t$:
$$t = 2(2) - 5 = 1$$
Now to see if these work in (1):
$$3(-1) + 3 = 2 - 2 \; \color{green}{\checkmark}$$
If we plug our parameters into their respective vector forms we get the same point, the point of intersection:
$$ \begin{align} (3(-1)+3, -1, -1+3) &= (0, -1, 2) \\[5pt] (2-2, 2(2)-5, 2) &= (0, -1, 2) \end{align}$$
-
Determine whether the lines
$$ \begin{align} L_1: \; x &= 2t-1, \; y = 1-t, \; z = 3t \\[5pt] L_2: \; x &= s+1, \; y = 2s, \; z = 3-2s \end{align}$$
intersect
Solution
First equate the parametric versions of each of the $x, y$ and $z$ terms of each line:
$$ \begin{align} 2t - 1 &= s + 1 \tag{1} \\[5pt] 1 - t &= 2s \tag{2} \\[5pt] 3t &= 3 - 2s \tag{3} \end{align}$$
If we solve (1) for $s$ we get $s = 2t - 2$. Plugging that into (2) gives us
$$ \begin{align} 1 - t &= 2(2t - 2) \\[5pt] -t &= 4t - 4 - 1 \\[5pt] -5t &= -5 \; \rightarrow \; t = 1 \end{align}$$
Plugging $t = 1$ back into (1) gives $s = 0$. Now to see if these work in (3)
$$3(1) = 3 - 0 \; \color{green}{\checkmark}$$
If we plug our parameters into their respective vector forms we get the same point, the point of intersection:
$$ \begin{align} (2(1)-1, 1-1, 3(1)) &= (1, 0, 3) \\[5pt] (0+1, 2(0), 3-2(0)) &= (1, 0, 3) \end{align}$$

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2016-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.