Geometric situations
The geometric distribution is related to the binomial distribution. In the latter, we considered the probability of $x$ "successes" occuring after $n$ trials with a fixed binary probability of success of $p$. In the geometric distribution, we ask a slightly different question: In a series of binomial trials with fixed probability (Bernoulli trials), what is the probability that success will occur on the xth trial?
This is often a useful question to ask. For example, in the U.S., about 6% of all physicians (there are about a million of them at any given time) are pediatricians. So we might ask, "What is the probability that if I query physicians randomly, the fifth one will be a pediatrician?" We'll figure out how to answer that question here.
The geometric distribution
If the probability of success in a geometric situation is $p$, then the probability of failure — provided that each trial is independent of the others — is $1-p$. If we're asking for the probability that success occurs on the xth trial, then we need to have failure on the first $x-1$ trials, then the success. Mathametically that is
$$P(X=x) = (1-p)^{x-1} p ,$$
where $X$ is our random variable, and $x$ is the value of $X$ for which we seek the probability.
In our example above that proabability would be
$$ \begin{align} P(X=5) &= (1-p)^{x-1} p \\[5pt] &= (1-0.06)^{5-1}(0.06) \\[5pt] &= 0.94^4 (0.06) = 0.0468 \end{align}$$
or about a 4% chance.
Now let's look at a portion of the distribution by calculating probabilities of finding a pediatrician on the first, second, third, and so on ... trials.
Probability that the nth doctor is a pediatrician
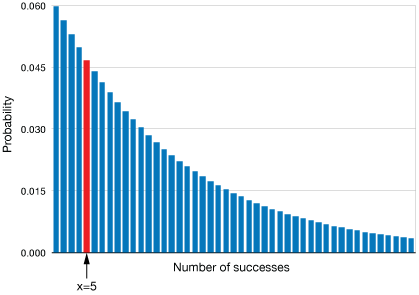
Notice a few things about this graph:
- The random variable $X$ is unbounded. We can calculate probabilities for any value of $X \ge 1$.
- In this situation, we are most likely ($P=6%$) to find a pediatrician in the first doctor we ask. Then the probabilities diminish.
- By summing these probabilities, we can calculate, for example, the probability that we find a pediatrician within the first 5 doctors we ask.
Geometric distribution
The probability of success after $x$ trials of a binary (Bernoulli) experiment with probability of success $p$ is
$$P(X=x) = (1-p)^{x-1} p$$
where $x = 1, \; 2, \; 3, \; \dots$.
The mean and variance of this distribution is
$$\mu_X = \frac{1-p}{p} \phantom{000} \text{and} \phantom{000} \sigma^2 = \frac{1-p}{p^2}$$
Example 1
Consider flipping a fair coin. Calculate the probabilies that
- Obtaining the first "heads" on the third flip.
- Obtaining heads in the first three flips.
$$ \begin{align} P(X=3) &= (1-p)^{3-1}p \\[5pt] &= (1-0.5)^2 0.5^1 \\[5pt] &= 0.125 = 12.5\% \end{align}$$
The probability of tossing heads for the first time on the third flip is 12.5%.
(b) The probability of tossing heads in either toss 1, 2 or 3 is the sum of probabilities,
$$P(X=1) + P(X=2) + P(X=1)$$
That is
$$ \begin{align} P &= 0.5^2 \cdot 0.5 + 0.5^1 \cdot 0.5 + 0.05^0 \cdot 0.5 \\[5pt] &= 0.125+0.250+0.5 = 0.875 \end{align}$$
There is an 87.5% chance that the first heads will be thrown within the first three tosses. Here's a graph of the distribution. The red bars represent the total probability referred to in part (b).
Geometric distribution, $p=0.5$

Example 2
A company with a computer network experiences network failures in about 10% of weeks. Let's say that the leaders of the company would like to know the probability that the company can go 5 weeks or longer without experiencing a failure.
$$ \begin{align} P(X=5) &= (1-p)^{5-1}(p) \\[5pt] &= (1-0.1)^{5-1}(0.1) \\[5pt] &= 0.0656 \approx 6.6\% \end{align}$$
If we'd wanted to know the probability that a network failure (a "success" in this problem) would occur in the sixth week, we'd caclulate
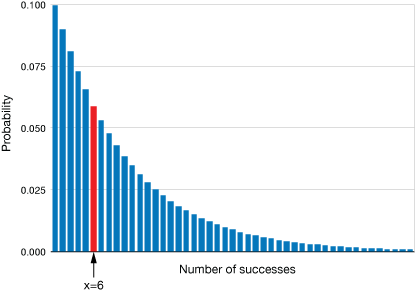
$$ \begin{align} P(X=6) &= (1-p)^{6-1} p \\[5pt] &= (1-0.1)^5 (0.1) \\[5pt] &= 0.059 \approx 6\% \end{align}$$
There would be about a 6% chance of the failure falling in week 6. To get the proabability that the network would last longer than 5 weeks, we'll have to sum the first five probabilities, then subtract the sum from 1:
$$ \begin{align} P(X\gt 5) &= 1-[P(X=1) + P(X=2) + \\[5pt] &P(X=3) + P(X=4) + P(X=5)] \\[5pt] &= 1-[0.9^4(0.1)+0.9^3(0.1)+0.9^2(0.1) + \\[5pt] & \phantom{000} 0.9^1(0.1) + 0.9^0(0.1)] \\[5pt] &= 0.5905 \approx 60\% \end{align}$$
So there's about a 60% chance that the network will operate failure-free for longer than 5 weeks.
Here's a look at the binomial distribution with $p=0.1$. The bar for $X=6$ is highlighted.
Geometric distribution, $p=0.1$
Practice problems
-
Consider rolling a six-sided die.
- Calculate the probability that a five is rolled for the first time on the third roll.
- Calculate the probability that a 4 is rolled more than twice before a 5.
- Calculate the mean number of rolls before rolling a 5, and its standard deviation.
Solution
Answer here
-
Consider rolling a six-sided die.
- Calculate the probability that a five is rolled for the first time on the third roll.
- Calculate the probability that a 4 is rolled more than twice before a 5.
- Calculate the mean number of rolls before rolling a 5, and its standard deviation.
Solution
Answer here

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.