Periodic functions → many solutions
Often we are faced with solving equations involving trigonometric equations, like $\sin(x) = 1/2$. Because of the periodic nature of the trigonometric functions – they repeat themselves infinitely many times – the variable x can take on an infinite number of solutions.
Here's an example, $\sin(x) = \sqrt{2}/2$. We know that $\sin(\pi/2) = \sqrt{2}/2$, but so do $\sin(3\pi/2), \, \sin(9\pi/2), \, \sin(11\pi/2)$, and so on ... see the graph below. The solutions to the equation are the intersections of the function $f(x) = \sin(x)$ and $g(x) = \sqrt{2}/2$.
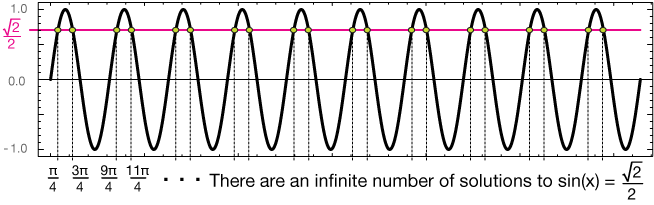
While it is possible to communicate to a reader the infinite set of all solutions to such equations, , we usually just restrict the domain to only a small region so that the number of solutions is finite. For example, we might need the solutions to $sin(x) = 1/2$ on the interval $[0, \, \pi]$ or the interval $(-\pi/2, \, \pi/2)$.
In this section we'll do several examples of trig-equation solving, and eventually I'll put some videos up to help you. But first, there are a few tools you'll need to have at your disposal ...
Tools you'll need to solve trig equations
In order to be effective solving trigonometric equations, there are some things you'll just have to know first. If you don't, now's the time to review them.
- You have to know the sines, cosines and tangents of the common angles (0, π/4, π/2, 3π/4, π, 5π/4, 3π/2, 7π/4, 2π) in radians.
- It's crucial that you are able to make a quick sketch – on paper or in your head – of one or more cycles of each of the three basic trig functions. That means knowing both the general shapes of the curves, that sine starts at zero and cosine starts at +1, and that the tangent is a repeating sigmoid (sideways S-shaped) curve.
- You should be able to jot down the common angles, in multiples of π/4 and π/6. I've only included the π/4 angles in these figures, you'll get a refresher on the others if you work through the examples below. Sketching these graphs is really just a matter of counting, much as you'd do for the unit circle. Start by writing 0 and 2π, then divide that into chunks of π, then π/2, then divide each of those into π/4 or π/6 pieces.
- You'll need to know your analytic trigonometry, mainly the Pythagorean identities and a few others that can be very helpful. At least be able to quickly look up the double angle and trig. sum formulas.
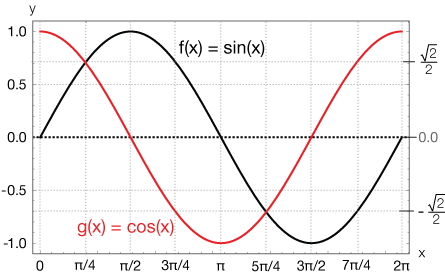
You should be able to easily sketch a cycle of the sine and cosine functions like this. They don't need to be as neat or detailed, but being able to make these quick sketches can go a long way toward reminding you of the details you'll need to solve trig equations.
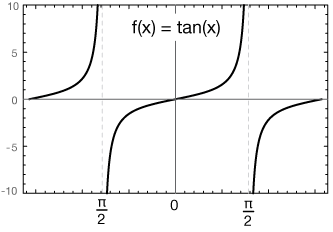
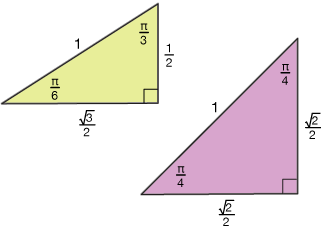
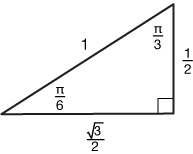
To further refresh you memory, here are a graph of a couple of cycles of the tangent function (remember, it has asymptotes because the denominator, cos(x), is zero at multiples of π), and the most important right triangles, 45-45-90 and 30-60-90.
Example 1
Solve the equation $\tan(x) = \sqrt{3}$ on the interval $[-2\pi, \, 2\pi]$.
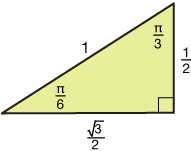
Now notice that

Now here's a graph of $\tan(x)$ between $[-2\pi, \; 2\pi]$. On it, we'll plot our initial solution, $x = \sqrt{3}/3.$
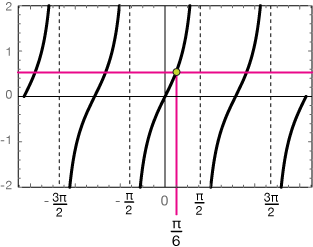
The magenta line is the line $y = \sqrt{3}.$ Obviously, on $[-2\pi, \; 2\pi]$ there are three additional solutions, places where the tangent function is equal to $\sqrt{3}.$ We need to find those. Fortunately, the tangent function has very regular behavior, which just reduces the rest of the problem to some simple arithmetic. Notice that every curve in the tangent graph is separated by $\pi$ radians. That means our solutions, one per curve, are $\pi$ rad apart. So we just need to add multiples of $\pi$, or better yet $6\pi/6$ for the common denominator, like this:
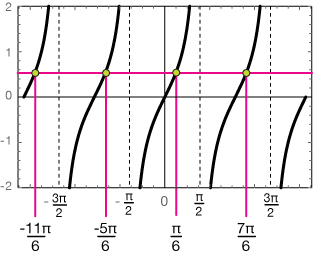
So on our interval, $[-2\pi, \; 2\pi]$, we have four solutions to this trig equation. They are:
$$x = \frac{-11\pi}{6}, \; \frac{-5\pi}{6}, \; \frac{\pi}{6}, \; \frac{7\pi}{6} \;$$
We found these by first finding one solution, the easiest, which we found by remembering the 30-60-90 triangle, then we recognized the periodicity of the tangent function – repeating every $\pi$ radians – to walk through our interval and count out the rest of the solutions.
Example 2
Solve the equation $2 \sin(x) = \sqrt{x}$ on the interval $[0, \, 4\pi]$.
$$2 \sin(x) = \sqrt{2}$$
In this case, that's dividing by 2 on both sides:
$$\sin(x) = \frac{\sqrt{2}}{2}$$
Now hopefully that $\sqrt{2}/2$ will trigger the memory of the 45-45-90 triangle, and how we can use it to find trig functions for 45˚ angles.
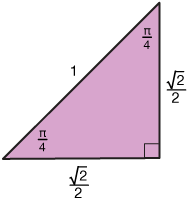
So we have as our basic solution
$$x = \frac{\pi}{4}$$
Now let's sketch a graph of the sine function between 0 and 4π. We'll sketch in the line $y=\sqrt{2}/2$ and notice that we should have four solutions to our equation on this interval, one for every intersection of the line an the curve.
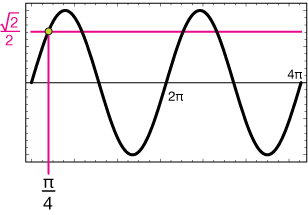
Now all that's left is to recognize that these solutions will have a repeating pattern. For each cycle of the sine curve, there will be a solution at $\pi/4$ radians and one at $3\pi/4$ – that much we recall by knowing what one cycle of $\sin(x)$ looks like. The other two solutions are just $\pi/4$ and $3\pi/4$ rad away from the start of the second cycle, at $2\pi$, so they're $2\pi+\pi/4$ and $2\pi+3\pi/4$.
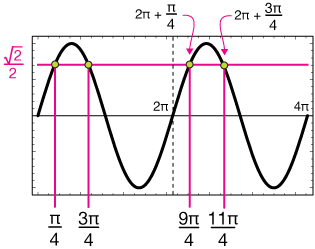
So this equation has four solutions on the interval [0, 4π]. They are:
$$x = \frac{\pi}{4}, \; \frac{3\pi}{4}, \; \frac{9\pi}{4}, \; \frac{11\pi}{4} \;$$
Example 3
Solve the equation $cos^2(2x) - 1 = 0$ on the interval $[-\pi, \, \pi]$.
$$\cos^2(2x) - 1 = 0$$
Moving the 1 to the right gives us
$$\cos^2(2x) = 1$$
And taking the root of both sides yields:
$$\cos(2x) = ± 1$$
The first thing you might want to do from here is look for a double-angle identity, like
$$\cos(2x) = \cos^2(x) - \sin^2(x)$$
That would be fine, but if you recall that $\cos(2x)$ is just a transformed version of $\cos(x)$ with two complete cycles of the function between 0 and $2 \pi$;.
That means, for our purposes, that there is a complete cosine cycle between 0 and $\pi$, and because cos(x) is an even function [meaning $f(-x) = (x)$], it has mirror symmetry across the y-axis. Here's what the graph looks like:
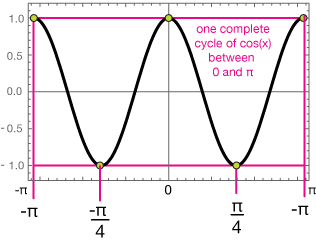
Our first solution is $x = 0$; then it's just a matter of noting that there's a solution to this equation every $\pi/4$ radians, so our solutions on the interval $[-\pi, \; \pi]$ are
$$x = -\pi, \; \frac{-\pi}{2}, \; 0, \; \frac{\pi}{2}, \; \pi$$
Practice problems
Solve the following trigonometric equations analytically on the interval $[0, \, 2\pi]$
-
$$\sin(x) = 1/2$$
Solution
The 1/2 should bring to mind the 30-60-90 triangle, which shows us that the sine of 30˚ (π/6) is 1/2.
The obvious solution is π/6, but if we sketch out sin(x) we see that there are three more solutions on this interval, labeled A, B and C
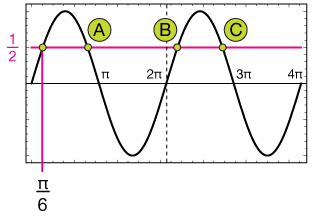
Finding the other solutions is a matter of using the symmetry of the sine function. Solution B is π/6 units back from π, and so forth:
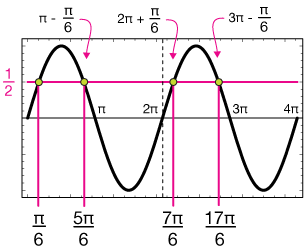
The solutions are
$$x=\frac{\pi}{6}, \; \frac{5\pi}{6}, \; \frac{7\pi}{6}, \; \frac{17\pi}{6}$$
-
$$\sqrt{3} \cdot \text{cot}(x) + 1 = 0$$
Solution
A good strategy for a problem like this is to isolate the trig. function, which gives.
$$\text{cot}(x) = \frac{-1}{\sqrt{3}}$$
Now the cotangent might be awskard to work with, so take the reciprocal of both sides to convert to tangent (you should know how to sketch several cycles of tan(x)):
$$\tan(x) = -\sqrt{3}$$
Now the $\sqrt{3}$ should remind you of the 30-60-90 triangle, for which the tanbent of π/6 is $\sqrt{3}$:

Now we want $-\sqrt{3}$, but that's not to hard: just sketch out the tangent function and notice thhat it has some symmetry: tan(-π/6)=$-\sqrt{3}$. so that's our first, or "prototype" solution:
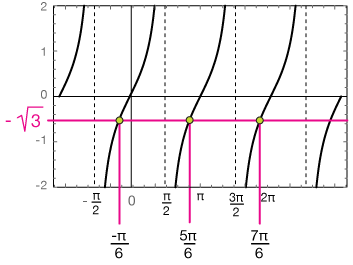
All solutions are obtained by going to the zero of each tan(x) curve and "backing up"e; (subtracting) π/6 units. The only ones in the [0, 2π] interval are:
$$x = \frac{5\pi}{6}, \; \frac{7\pi}{6}$$
-
$$2 \, \sin(x) + \sqrt{3} = 0$$
Solution
A good strategy for a problem like this is to isolate the trig. function, which gives
$$\sin(x) = \frac{-\sqrt{3}}{2}$$
Now the $\sqrt{3}{2}$ should remind you of a 30-60-90 triangle, for which the sine of π/3 is $\sqrt{3}/2$.

Now we want $-\sqrt{3}{2}$, but that's not too hard — just sketch out the sine function and notice that it has some symmetry: sin(-π/3) = $-\sqrt{3}{2}$. That solution is out of our domain, but notice that it's π/3 units from the zero of sin(x):
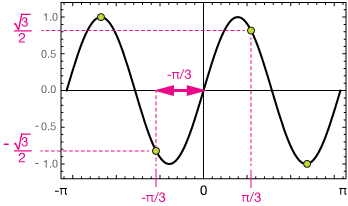
so there are two solutions on the interval [0, 2π]. One is π/3 to the right of zero, the other π/3 to the left of 2π
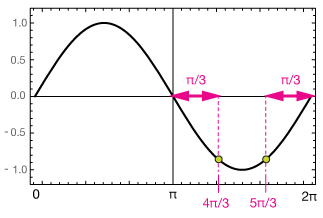
$$x=\frac{4\pi}{3}, \; \frac{5\pi}{3}$$
-
$$\text{sec}^2(x) - 1 = 0$$
Solution
First isolate the trig. function on the left:
$$\text{sec}^2(x)=1$$
Take the root of both sides (dont' forget the $\pm$).
$$\text{sec}(x)=\pm 1$$
Now convert to one of the big three trig. functions (sin, cos, tan) to make it easier to visualize the solutions:
$$ \begin{align} \frac{1}{\cos(x)} &=\pm 1 \\[5pt] \cos(x) &= \pm 1 \end{align}$$
Now sketch the cosine function and notice that there are three places where cos(x) = ±1 on the interval [0, 2π]
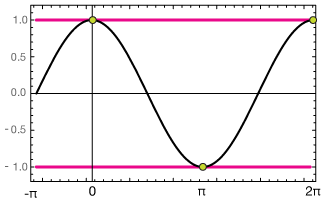
So the solutions are
$$x=0, \; \pi, \; 2\pi$$
-
$$2 \cos(x) - \sqrt{3} = 0$$
Solution
Shoot the constants to the right side using good algebra moves:
$$\cos(x) = \frac{\sqrt{3}}{2}$$
Now the $\sqrt{3}/2$ should remind you of the 30-60-90 triangle, for which the cosine of π/6 is $\sqrt{3}\pi/2$.

Sketch out one cycle of the cosine function and identify where it's y-coordinate is $\sqrt{3}/2$:
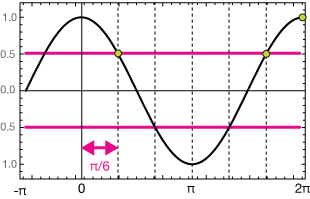
The solutions are
$$x=\frac{\pi}{6}, \; \frac{11 \pi}{6}$$
-
$$\tan(x) = 1$$
Solution
This equation is already in very simple form. To find tan(x)=1, we recall the 45-45-90 triangle
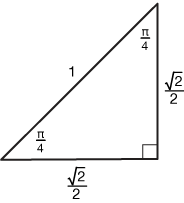
So tan(π/4)=1. That's our "prototype" solution. Now we need to sketch the graph of tan(x) between 0 and 2π.
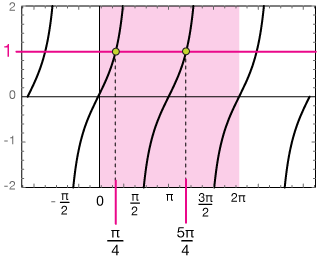
The solutions are π/4 units to the right of every zero of the tangent curves, so in this interval, the two solutions are
$$x=\frac{\pi}{4}, \; \frac{5\pi}{4}$$
-
$$\text{csc}^2(x) = 1$$
Solution
Take the root of both sides, and don't forget the ±1:
$$\text{csc}(x)= \pm 1$$
Now express csc(x) in terms of sin(x), then take the reciprocal of both sides to end up with a much simpler equation:
$$ \begin{align} \frac{1}{\sin(x)} &= \pm 1 \\[5pt] \sin(x) &= \pm 1 \end{align}$$
Now it's easy to see that there are two solutions on the interval [0, 2π]. One is at x = π/2 and the other at 3π/2.
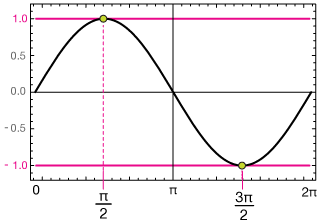
$$x=\frac{\pi}{2}, \; \frac{3\pi}{2}$$
-
$$\tan(x) + 1 = 0$$
Solution
Isolate the trig. function on the left side:
$$\tan(x)=-1$$
The equation tan(x)=1 (positive one) should make you think of the 45-45-90 triangle:

Now the tangent of π/4 is 1. Let's draw the tangent function between 0 and 2π and use its symmetry to find the locations where tan(x) = -1.
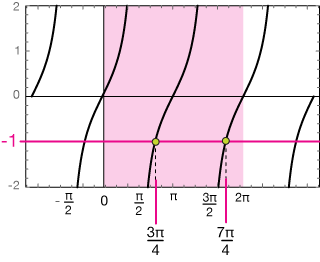
The solutions are π/4 units to theh left of every zero of the tangent curves, so in this interval, the two solutions are
$$x = \frac{3\pi}{4}, \; \frac{7\pi}{4}$$
analytically
In this context, analytically means "on paper with a pencil or pen." That is, we can solve the problem exactly without a computer.

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.