This section is related to sections on the integral test and p-series for convergence of infinite series. Understanding the material in this section will help you understand series convergence.
What's so improper?
The integrals we'll work on in this section aren't literally "improper," like maybe you shouldn't do them, they're just a little different. They're basically integrals for which one or both limits aren't strictly defined, or that have a discontinuity somewhere between the limits of integration.
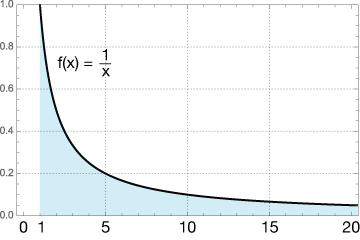
For example, what if we wanted to know the area under the curve $f(x) = \frac{1}{x}$ between the limits of x = 1 and x → ∞ ? We might write that integral like this:
$$\int_1^{\infty} \, \frac{1}{x} \, dx,$$
but a better way to write it is
$$\lim_{t \rightarrow \infty} \, \int_1^t \, \frac{1}{x} \, dx.$$
As a reminder, the area we're looking for is:
Now this is an integral we can do easily:
$$ \begin{align} \lim_{t \rightarrow \infty} \, &\int_1^t \, \frac{1}{x} \, dx \\[5pt] &= \lim_{t \rightarrow \infty} \, ln|x| \bigg|_1^t \\[7pt] &= \lim_{t \rightarrow \infty} \, ln|t| - 0 \: \rightarrow \: \infty \end{align}$$
When the limit is evaluated, we see that the area under this curve is infinite. That's not too surprising given that we know that y = 0 is an asymptote, and that the function approaches but never quite reaches a value of zero as $x \rightarrow \infty.$ What's interesting is that similar functions do bound a finite area. We'll see one in the next example.
We say that this integral diverges. If one or both limits of an improper integral is infinite or doesn't exist, the integral diverges. An improper integral that has a finite limit is said to converge to that limit.
Example 2
Calculate the value of the area under $f(x) = \frac{1}{x^2}$ from x = 0 to infinity.
The integral is
$$\lim_{t \rightarrow \infty} \, \int_1^t \, \frac{1}{x^2} \, dx.$$
This again is not a difficult integral to evaluate:
$$ \begin{align} \lim_{t \rightarrow \infty} \, &\int_1^t \, \frac{1}{x^2} \, dx \\[5pt] &= \lim_{t \rightarrow \infty} \; -\frac{1}{x} \, \bigg|_1^t \\[5pt] &= \lim_{t \rightarrow \infty} \; \frac{-1}{t} + 1 = 1 \; unit^2 \end{align}$$
So this curve, very similar to the one in our first example above, encloses a finite area, even though the function still approaches the x-axis asymptotically as x grows. Strange.
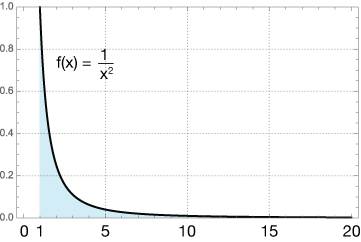
We say that an improper integral like this converges to a finite value. The interpretation of these two results that makes the most sense is that the second function approaches zero more rapidly, and apparently sufficiently fast that it encloses a finite area. You'll find a somewhat more satisfying interpretation in the section on the integral test for infinite series.
More on convergence & divergence
The first two examples here show how two similar functions can enclose finite and infinite areas, even though they both behave asymptotically &emdash; that is, they both approach a steady value but never actually reach it. That can be a difficult thing to wrap your mind around.
To help you visualize what's going on, take a look at some sum of our expressions, 1/n and 1/n2 as n grows by factors of two. The first row is the first term, the second is the sum of the first 10 terms, and so on:
| $n$ | $1/n$ | $1/n^2$ |
| 1 | 1.00000000 | 1.00000000 |
| 10 | 2.92896825 | 1.54976773 |
| 20 | 3.59773966 | 1.59616324 |
| 40 | 4.27854304 | 1.62024396 |
| 80 | 4.96547928 | 1.63251187 |
| 160 | 5.65551122 | 1.63870356 |
| 320 | 6.34709835 | 1.64181394 |
| 640 | 7.03946489 | 1.64337279 |
| 1280 | 7.73222160 | 1.64415312 |
| converges |
And below is a graph of these growing sums.
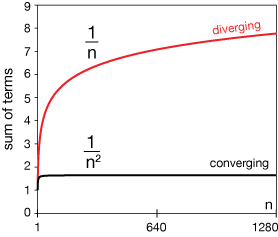
You can see that the sum of terms of the form 1/n2 grows rapidly at first, then approaches a limit. In fact, the three digits after the decimal will settle in to .644 and never change thereafter. Further terms just refine digits successively to the right of the decimal. In contrast, the sum of terms of the form 1/n, the so-called harmonic series, continues to grow. In fact, it can be shown that this sum can be used to represent any number if we just add enough terms. That's the difference between divergence and convergence.
One way to think of it, if it helps, is that one denominator approaches infinity "faster" than the other, and that makes the difference.
This concept of convergence and divergence is central to many aspects of mathematics, including how computers and calculators compute things like sines, cosines and logarithms.
The p-integral
We can expand on the previous two examples to ask, for what value of p does the integral $\int_1^{\infty} \, \frac{1}{x^p} \, dx$ converge?
The integral is
$$ \begin{align} \lim_{t \rightarrow \infty} \, \int_1^t \, \frac{1}{x^p} \, dx &= \lim_{t \rightarrow \infty} \, \frac{x^{-p + 1}}{1 - p} \, \bigg|_1^t \\[5pt] &= \frac{1}{1 - p} \, \lim_{t \rightarrow \infty} \left[ t^{-p + 1} - 1 \right] \\[5pt] &= \frac{1}{1 - p} \, \lim_{t \rightarrow \infty} \left[ \frac{1}{t^{p - 1}} - 1 \right] \end{align}$$
Now the fraction goes to zero as $t \rightarrow \infty$ as long as $p \gt 1,$ so as long as $p \gt 1,$ the integral has a finite value of $\frac{1}{p - 1}.$
This is a refinement in our understanding of the convergence of the area under functions like $f(x) = 1/x^p.$ As long as $p \gt 1,$ the area is finite and can be calculated.
Example 3
Now let's consider the integral of a function with a discontinuity. Compute the integral
$$\int_3^7 \, \frac{1}{\sqrt{x - 3}} \, dx$$
The function is infinite at x = 3, so we'll need to rewrite it, approaching the limit x = 3 from above or from inside the area being integrated, like this,
$$\lim_{t \rightarrow 3^+} \, \int_t^7 \, \frac{1}{\sqrt{x - 3}} \, dx$$
Now the integral is done by u-substitution to yield
$$ \begin{align} &= \lim_{t \rightarrow 3^+} \, 2 \sqrt{x - 3} \, \bigg|_t^7 \\[5pt] &= 2(\sqrt{4} - 0) = 4 \end{align}$$
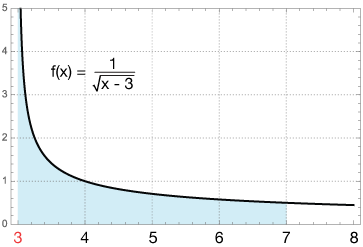
Notice that for this integral, once we found the antiderivative, our discontinuity wasn't a problem any more, and simply performing the integral without regard to it would have worked. Nevertheless, it's important to be aware of discontinuities and make sure that any integral over one converges to a real value.
Example 4
Compute the integral of $f(x) = ln(x)$ between $x = 0$ and $x = 1.$
This is a tricky problem because ln(0) is undefined. Its domain is (0, ∞). Here's the graph of y = ln(x):
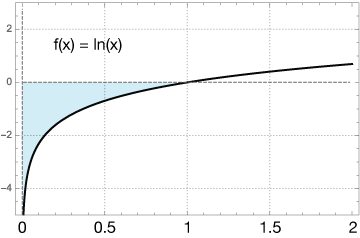
The integral is
$$\lim_{t \rightarrow 0^+} \, \int_t^1 \, ln(x) \, dx$$
You might recall that this integral can be done by parts; the antiderivative of $ln(x)$ is $x \, ln(x) + x + C,$ so our limit is
$$ \begin{align} \lim_{t \rightarrow 0^+} &[x \, ln(x) + x] \, \bigg|_t^1 \\[5pt] &= 1 \cdot ln(1) - 1 - \lim_{t \rightarrow 0^+} \, [t \, ln(t) - t] \\[5pt] &= -1 - \lim_{t \rightarrow 0^+} \, [t \, ln(t) - t] \\[5pt] &= -1 - \lim_{t \rightarrow 0^+} \, t \, ln(t) \end{align}$$
Now the remaining limit can be evaluated as an ∞/∞ limit using L'Hopital's rule:
$$ \begin{align} \lim_{t \rightarrow 0^+} \, t \, ln(t) &= \lim_{t \rightarrow 0^+} \, \frac{ln(t)}{1/t} \\[5pt] &= \frac{1/t}{-1/t^2} = -t \: \rightarrow \: 0 \end{align}$$
So remembering the -1 from our original limit, the result is -1. The shaded area of our integral is 1 square unit, lying below the x axis. The integral converges to a finite value.
Example 5
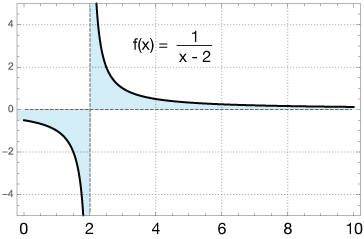
Consider the integral of a function with a discontinuity within the interval of integration.
Integrate
$$f(x) = \frac{1}{x - 2}$$
between $x = 0$ and $x = 10.$
Here's a graph of the function and the area we're trying to find:
Let's first think about this integral as if we didn't know about the discontinuity. It's pretty simple:
$$ \begin{align} \int_0^{10} \, \frac{1}{x - 2} \, dx &= ln |x - 2| \, \bigg|_0^{10} \\[5pt] &= ln|8| - ln|2| = ln \left| \frac{8}{2} \right| = ln(4) \end{align}$$
But this isn't correct, as we'll see. Now let's do the integral but this time consider the vertical asymptote at x = 2.
$$ \begin{align} &\lim_{t \rightarrow 2^-} \, int_0^t \, \frac{dx}{x - 2} + \lim_{t \rightarrow 2^+} \, int_t^{10} \, \frac{dx}{x - 2} \\[5pt] &= \lim_{t \rightarrow 2^-} ln|x - 2| \bigg|_0^t + \lim_{t \rightarrow 2^+} ln|x - 2| \bigg|_t^{10} \\[5pt] &= \lim_{t \rightarrow 2^-} ln|t - 2| - ln(2) \\[5pt] &\phantom{0000} + ln(8) - \lim_{t \rightarrow 2^+} ln|t - 2| \end{align}$$
Now both of those limits evaluate to ln(0), which is infinite, so this integral diverges, and the area it encloses is infinite. So you can see that we need to consider the discontinuity.
Pro tip:
Integrals with infinite limits, like
$$\int_a^{\infty} \, f(x) \, dx, \: \: \text{ or } \: \: \int_{-\infty}^{a} \, f(x) \, dx, \: \: \text{ or } \: \: \int_{-\infty}^{\infty} \, f(x) \, dx$$
are sometimes called Type 1 improper integrals in books and articles. Likewise, those without infinite limits, but with a discontinuity somewhere inside the interval of integration are called Type 2 improper integrals.
Practice integrals
Calculate the value of the following integrals, or show that they diverge.
-
$$\int_{-1}^1 \, \frac{1}{x^2} \, dx$$
Solution
Here is the graph of our function:
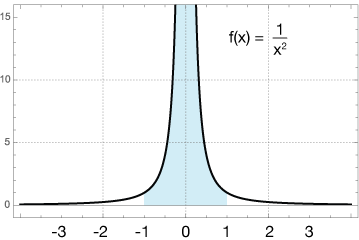
First, we can consider the symmetry of the problem, and reduce our integral twice the area below the function between x = 0 and x = 1:
$$A = 2 \, \lim_{t \rightarrow 0^+} \, \int_t^1 \, \frac{1}{x^2} \, dx$$
This is a fairly simple integral to do (express the fraction as x-2 and use the power rule). The result is
$$= 2 \, \lim_{t \rightarrow 0^+} \, \left[ \frac{-1}{x} \right]_t^1 = 2 \left( \frac{-1}{1} \right) - 2 \lim_{t \rightarrow 0^+} \frac{-1}{t}$$
Now the limit on the right is infinite, so this integral diverges, and we can't calculate a finite area.
-
$$\int_{0}^1 \, \frac{ln(x)}{\sqrt{x}} \, dx$$
Solution
Here is the graph of our function:
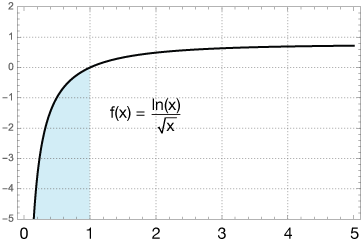
Like $f(x) = ln(x),$ this function approaches -∞ as x approaches zero from above. Our integral is
$$A = 2 \, \lim_{t \rightarrow 0^+} \, \int_t^1 \, \frac{ln(x)}{\sqrt{x}} \, dx$$
To tackle the integral, let $u = \sqrt{x},$ then $u^2 = x,$ and $du = \frac{1}{2}x^{-1/2},$ so we have (forgetting the limits for now):
$$= 2 \, \int \, ln(u^2) \, du = 4 \, \int \, ln(u) \, du.$$
Now the antiderivative of ln(x) is $x ln(x) + x + C,$ so we have
$$ \begin{align} & 4 u \, ln(u) + u \; \rightarrow \\[5pt] & \lim_{t \rightarrow 0^+} \, 4 \left[ \sqrt{x} \, ln(\sqrt{x}) - \sqrt{x} \right]_t^1 \\[5pt] &= -1 - \lim_{t \rightarrow 0^+} \, \left[ \sqrt{t} \, ln(\sqrt{t}) - \sqrt{t} \right] \end{align}$$
Now we have to be careful here because the limit
$$\lim_{t \rightarrow 0^+} t \, ln(\sqrt{t})$$
is an indeterminate form, and we have to evaluate it using L'Hopital's rule. To do that we employ a trick to make the limit an ∞/∞ limit:
$$ \begin{align} &\lim_{t \rightarrow 0^+} \, \frac{ln(\sqrt{x})}{\frac{1}{x}} \\[5pt] &= \lim_{t \rightarrow 0^+} \, \frac{{t^{1/2} \left(\frac{1}{2}\right)t^{-1/2}}}{-t^{-2}} \\[5pt] &= \lim_{t \rightarrow 0^+} \, \frac{\frac{1}{2t}}{\frac{-1}{t^2}} \\[5pt] &= lim_{t \rightarrow 0^+} \, \frac{-t}{2} = 0 \end{align}$$
In the second step, we took the derivatives of the numerator and denominator, accoroding to L'Hopital's rule. Now if we remember our -1 from earlier, we see that the area is -1 units2. This is a good problem to study.
-
$$\int_{0}^{\infty} \, \frac{e^x}{e^{2x} + 1} \, dx$$
Solution
Here is the graph of our function:
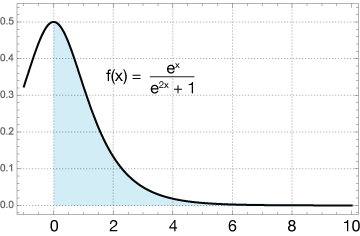
This is an improper integral simply because of the infinite upper bound. The integral is
$$A = \lim_{t \rightarrow \infty} \, \int_0^t \, \frac{e^x}{e^{2x} + 1} \, dx$$
This integral can be done by substitution. Let $u = e^x,$ then $du = e^x \, dx$ and $u^2 = e^{2x}.$ We can swap limits and stick with u: when $x = 0, \; u = 1,$ and when $x \rightarrow \infty, \; u \rightarrow \infty.$ Our integral is then
$$A = \lim_{t \rightarrow \infty} \, \int_0^t \, \frac{1}{u^2 + 1} \, du$$
Now recall that $\frac{d}{dx} \text{tan}^{-1}(x) = \frac{1}{x^2 + 1},$ so we have
$$ \begin{align} A &= \lim_{t \rightarrow \infty} \, \text{tan}^{-1}(u) \\[5pt] &= \lim_{t \rightarrow \infty} \, \text{tan}^{-1}(t) - \text{tan}^{-1}(1) \\[5pt] &= \frac{\pi}{2} - \frac{\pi}{4} = \frac{\pi}{4} \; units^2 \end{align}$$
The area under this curve from x=0 to x=∞ is finite.
-
$$\int_{0}^5 \, \frac{x}{x - 1} \, dx$$
Solution
Here is the graph of our function:
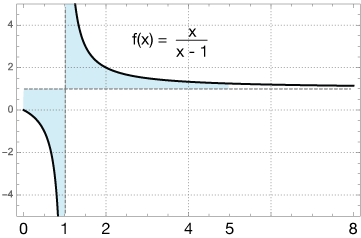
This is an improper integral because of the discontinuity at x = 1. Notice that if we just did the integral in a straightforward way, ignoring the vertical asymptote, we could do it by substitution: let $u = x - 1,$ then $du = dx$ and $x = u + 1,$ so we have
$$ \begin{align} A &= \int_{-1}^4\, \frac{u + 1}{u} \, du \\[5pt] &= \int_{-1}^4\, 1 + \frac{1}{u} \, du \\[5pt] &= u + ln|u| \, \bigg|_{-1}^4 \\[5pt] &= 4 + ln(4) + 1 - ln|-1| = 5 + ln(4) \end{align}$$
But this is not correct, as we shall see. The proper improper integral is
$$A = \lim_{t \rightarrow 1} \, \int_0^t \, \frac{x}{x - 1} \, dx + \lim_{t \rightarrow 1} \, \int_t^5 \, \frac{x}{x - 1} \, dx$$
Using the same substitution and swapping limits to u-limits, we have
$$ \begin{align} &\lim_{t \rightarrow 1} \int_{-1}^{t-1} \left(1 + \frac{1}{u} \right) du + \lim_{t \rightarrow 1} \int_{t-1}^{4} \left(1 + \frac{1}{u} \right) du\\[5pt] &= \lim_{t \rightarrow 1} u + ln|u|\bigg|_{-1}^{t-1} + \lim_{t \rightarrow 1} u + ln|u| \bigg|_{t-1}^4 \end{align}$$
This expression will contain two terms like
$$\lim_{t \rightarrow 1} \, ln|t - 1|,$$
so the limit is infinite, as is the area. The integral diverges.
-
$$\int_{0}^{\infty} \, x \, e^{-3x} \, dx$$
Solution
Here is the graph of our function:
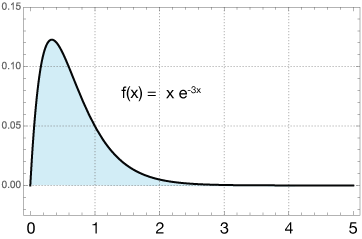
This is an improper integral because of the infinite upper limit. The improper integral is:
$$\lim_{t \rightarrow \infty} \, \int_0^t x \, e^{-3x} \, dx$$
We can do this integral by parts. Let $u = x,$ and $dv = e^{-3x} dx.$ Then $du = dx$ and $v = -\frac{1}{3} e^{-3x}.$ Then our integral becomes (forgetting the limits for now):
$$\lim_{t \rightarrow \infty} \, -\frac{x}{3} e^{-3x} + \frac{1}{3} \int e^{-3x} \, dx$$
Integrating and including the limits gives
$$= \lim_{t \rightarrow \infty} \, -\frac{x}{3} e^{-3x} - \frac{1}{9} e^{-3x} \, \bigg|_0^t.$$
Before evaluating the limits, it might be enlightening to rewrite that expression slightly, like this:
$$= \lim_{t \rightarrow \infty} \, -\frac{x}{3 e^{3x}} - \frac{1}{9 e^{3x}} \, \bigg|_0^t.$$
Now we can evaluate:
$$\lim_{t \rightarrow \infty} \, \frac{-t}{3 e^{3t}} - \frac{1}{9 e^{3t}} + 0 + \frac{1}{9}$$
The first limit can be evaluated using L'Hopital's rule. It reduces to zero. So our overal result is $\frac{1}{9}.$
-
$$\int_{-\infty}^{\infty} \, \frac{1}{1 + x^2} \, dx$$
Solution
Here is the graph of our function:
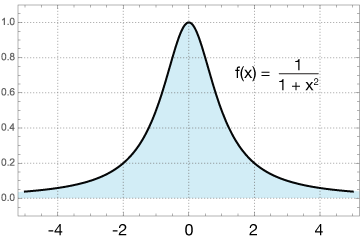
This is an improper integral because of the infinite limits. Because of the symmetry of the function, we can just integrate from 0 to ∞ and multiply by 2. The improper integral is:
$$2 \lim_{t \rightarrow \infty} \, \int_0^t \frac{1}{1 + x^2} \, dx$$
This is an inverse tangent integral. Recall that $\frac{d}{dx} \text{tan}^{-1}(x) = \frac{1}{x^2 + 1},$ so we have
$$2 \lim_{t \rightarrow \infty} \, \text{tan}^{-1}(x) \, \bigg|_0^t$$
The inverse tangent of zero is zero, and the inverse tangent of ∞ is π/2, so our limit is
$$= 2\lim_{t \rightarrow \infty} \, \text{tan}^{-1}(t) - \text{tan}^{-1}(0) = \pi \; units^2$$

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012-2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.