The language of geometry
There are many different flavors of geometry — maybe an infinite number. The kind that we'll deal with almost exclusively is called Euclidean Geometry, named after Greek geometer, Euclid. In Euclidean geometry nearly all action takes place on a 2-dimensional plane, but we can generalize a lot of Euclidean geometry into three (and higher!) dimensions.
This section will help you get familiar with most of the things you're likely to encounter in Euclidean geometry:
Euclidean geometry
Euclidean geometry is geometry in a plane, and involves planar figures like lines, triangles, circles etc.
Points
A point in Euclidean geometry is just a location in space. We can give it a name, a label (like a letter) or some coordinates, one for each dimension of the space we're in. For example, if we're talking about points on an x-y plane (called a Cartesian plane), points of the form $(x, y)$ will do it.
The point (3, 2) is located 3 units to the right of the origin (0, 0) and 2 units up. A point has no length; it is just a location.
A point is a location in space or on some object or figure.
We'll encounter the word "space" a lot in our study of geometry, and it has different meanings depending on the context. A line (below) is a one-dimensional space; we can only go in one direction or its negative (left being the negative of right, for example). A plane is a 2-dimensional (2-D) space; we can go in two different directions or their negatives, or any combination of both.
And we live in a 3-D world. A point is a zero-dimensional space. Interestingly, there are higher spaces of 4, 5, ... even an infinite number of dimensions, and we use them all the time to solve real problems. Oh, and time is never a dimension!

A line is kind of hard to define. It's one of those things: You know it when you see it.
Here's a try: A line is a collection of points such that, to travel upon it from one point to another provides the shortest possible path.
There are many other definitions that involve words like "straight" or the concept of a linear equation, but let's stick with "we know it when we see it." A line is a straight mark on the page that extends infinitely from both ends.
Lines can be labeled in two main ways, using two points or a general overall label for the whole line. In the diagram above we have line $\overline{AB}$ (which could also be written as $\overline{BA}.) and line $m$. These lines intersect at one and only one point.
Two lines may intersect at one point, an infinite number of points (in which case they're the same line) or never (in which case they're parallel).
A line segment is a finite section of a line that is bounded on either end by a point.
In this figure, we have line $\overline{BA}$, which includes segment $\overline{BA}$. And we have $\overline{CD}$ and triangle $XYZ$ ($\triangle XYZ$), which is composed of segments $\overline{XY}$, $\overline{YZ}$ and $\overline{YZ}$.
We almost always care more about line segments than lines in practical work, like in engineering, design or architecture.

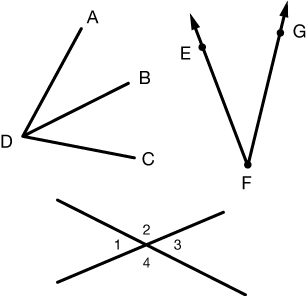
An angle is formed when two rays or two line segments join at a common point called the vertex of the angle. (A ray is half of a line).
We label angles with three letters (e.g. $ABC$) when there is any chance of ambiguity, and just a single letter when there is no chance of such confusion. We can also put a label inside an angle and call it that.
In this figure, we have on the upper left $\angle ABD$, $\angle BDC$ and $\angle ADC$. In this case we would not label any angle $\angle D$ because it's unclear which of the three we would mean.
On the upper right, we have $\angle EFG$ or just $\angle F$ (no chance of confusion with just one angle), and on the bottom we have four angles, $\angle 1$, $\angle 2$, $\angle 3$ and $\angle 4$.
Special angles: acute, right, obtuse, straight
Angles that measure less than 90˚ are called acute angles. 90˚ angles are right angles. Angles that measure more than 90˚ are obtuse angles and if we bend an angle all the way open to 180˚ so that it's just a line, it's sometimes called a straight angle.

Supplementary and Complementary Angles

← Supplementary angles sum to 180˚, a straight angle. While more than two angles can be supplementary, we usually just work with two that add to 180˚.
$$m \angle AXC + m \angle CXB = 180^{\circ}$$
Complementary angles sum to 90˚, a right angle.
$$m \angle MON + m \angle NOP = 90^{\circ}$$
(here the letter $m$ stands for measure: "$\angle ABC$" means "the measure of angle $ABC$".
Supplementary & complimentary angles
The measures of Supplementary angles sum to 180˚
The measures of Complementary angles sum to 90˚
Anatomy of a polygon
← Polygons are labeled using their vertices (plural of vertex). The pentagon might be called pentagon $ABCDE or polygon ABCDE.
The triangle is labeled $\triangle XYZ$, where the symbol $\triangle$ is a shorthand for "triangle".
Polygons may be regular or irregular. A regular polygon has sides of equal length (congruent sides) and angles of equal measure (congruent angles). Irregular polygons are composed of a mix of side lengths and angles.
A regular polygon is sometimes called an equilateral (equal-sides) polygon; we use this terminology most often to describe the equilateral triangle.

Polygons — interior and exterior angles
There are two important kinds of angles formed by the sides of any closed polygon, interior angles, illustrated below in a triangle, a square, a regular pentagon and a regular octagon.

Any closed polygon with $n$ sides has $n$ interior angles. The sum of the measures of those angles grows as we add sides. For example, the sum of the angles of a triangle is 180˚, while the sum of the angles of a square (or any four-sided polygon) is 270˚.
The exterior angles of a polygon are actually more useful. They are defined in the pictures below.
To form an exterior angle, extend one side outside of the polygon, then measure the angle to the next side, moving around the polygon in one direction. We're usually only concerned with one of the two exterior angles per vertex at a time.

The most useful property of exterior angles is that for any closed polygon, the sum of the exterior angles (taken one per side) is 360˚.
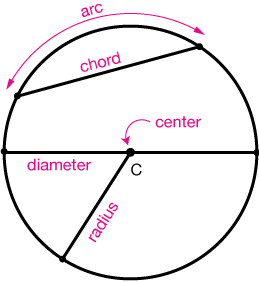
A circle is a collection of all points equidistant from a point called the center. A circle is generally labeled by refering to the label of the center point. This is circle C →.
A chord is a line that intersects a circle twice and a diameter is a chord that passes through the center of the circle.
A radius is half of a diameter; it extends from the center to any point on the circle. By the definition of a circle, all radii (plural of radius) are the same length.
An arc is any portion of a circle.
Circles are often identified with a circle symbol, $\bigodot$, and by their center point, such as $\bigodot A$.
These are definitions of just a few of the things you'll encounter as you study plane geometry. Other more specific concepts are defined in more detail in other sections. Have fun!

![]()
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012,2025, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.
